哈喽,大家好~
今儿再来和大家聊一个关于LSTM的案例:基于历史气象数据的LSTM气候预测。
全文内容,非常详细!~
首先说,LSTM(Long Short-Term Memory,长短期记忆)是一种特殊的递归神经网络(RNN),它能够有效解决标准RNN在处理长序列数据时,出现的梯度消失和梯度爆炸问题。因此,LSTM在处理具有时间依赖性的问题时(如时间序列预测、自然语言处理等)表现优异。
LSTM 核心原理
LSTM 的主要目标是记住长期信息并有选择性地遗忘无关的信息。它通过一个被称为“记忆单元”的结构,以及三个“门控机制”来实现这一目标。门控机制决定了哪些信息应该保存、哪些应该遗忘、哪些应该输出。
1. 记忆单元
LSTM 通过记忆单元来维护信息,这个记忆单元可以像容器一样,携带随时间变化的信息,并决定是否保留、更新或丢弃这些信息。LSTM 通过门控机制对记忆单元进行控制,从而允许网络对长时间前的信息保留或更新。
2. 三个门控机制
门控机制是 LSTM 中的关键部分,它们通过对信息流的控制来决定哪些信息被传递、哪些被遗忘。
具体来说,LSTM 有三个门控机制:
遗忘门(Forget Gate):决定当前时刻是否遗忘记忆单元中的某些信息。 输入门(Input Gate):决定当前时刻的新信息是否需要写入记忆单元。 输出门(Output Gate):决定当前时刻记忆单元中的信息是否用于最终输出。
每个门都是通过一个 sigmoid 函数和一些权重矩阵来控制的。sigmoid 函数的输出是一个在 0 到 1 之间的值,代表保留信息的比例。
LSTM 的工作原理
我们按时间步(time step)来看 LSTM 的工作流程。假设我们有一个时间序列输入(如时间步 、...),每个时间步,LSTM 执行以下操作:
步骤 1:计算遗忘门
遗忘门的作用是决定需要遗忘多少旧信息。它通过对上一个时间步的隐藏状态和当前时间步的输入进行加权,然后通过 sigmoid 函数,计算一个 0 到 1 之间的值。
是遗忘门的输出。 和 是权重矩阵和偏置项。 是将上一个隐藏状态 和当前输入 拼接在一起的结果。
遗忘门的输出 将会用来更新记忆单元的状态。 越接近 0,意味着将忘记之前的信息;越接近 1,表示保留更多之前的信息。
步骤 2:计算输入门和候选记忆
输入门决定新信息要写入多少到记忆单元中。
我们通过如下公式来计算:
这里, 是输入门的输出,表示新信息进入记忆单元的比例。
接着,LSTM 计算候选记忆单元(即可能更新的内容):
这里, 和 是新的权重矩阵和偏置项。这个候选记忆 会和输入门的输出 一起决定将多少新信息写入到记忆单元中。
步骤 3:更新记忆单元
LSTM 通过遗忘门和输入门的输出来更新记忆单元:
是更新后的记忆单元。 是上一个时间步的记忆单元。 表示保留之前记忆的部分。 表示要加入的新信息。
这样,LSTM 能够同时保留长时间依赖的信息,同时加入新的有用信息。
步骤 4:计算输出门和输出隐藏状态
最后,LSTM 通过输出门来决定当前时刻的输出信息,并更新隐藏状态:
这里, 是输出门的输出,表示当前记忆单元中的信息有多少要用来生成新的隐藏状态。
隐藏状态的更新方式是:
是当前时间步的隐藏状态。 是更新后的记忆单元状态。
隐藏状态 作为 LSTM 的输出,同时还会被传递到下一个时间步。
LSTM 工作流程
遗忘门决定遗忘多少旧信息。 输入门决定加入多少新信息。 更新记忆单元,保留重要信息并更新。 输出门决定当前的输出以及新的隐藏状态。
事实上,LSTM 类似于一个“记忆盒子”,它通过“门”机制(遗忘门、输入门、输出门)来灵活控制记忆的进出和保留。可以想象,LSTM 是一位有良好记忆力的学生,它会根据学习的内容决定哪些知识是重要的,需要长期记住,哪些信息是暂时的,可以在短时间后丢弃。
由于这种结构设计,LSTM 在处理长序列数据时非常有效,不会像普通的 RNN 那样,随着时间步数的增加,产生梯度消失或梯度爆炸的问题。
为什么 LSTM 能解决 RNN 的问题?
普通 RNN 在每个时间步上都会重复计算隐藏状态,信息容易随着时间步数的增加逐渐被遗忘,尤其是在处理长序列时,它很难“记住”较早的信息。这是因为随着网络层数和时间步的增加,RNN 容易出现梯度消失或爆炸,导致模型学习不到有用的长时间依赖。
而 LSTM 通过记忆单元和门控机制,允许模型选择性地保留重要信息,避免了信息随着时间推移完全消失,因此能够有效应对长时间序列的任务。
整体而言,LSTM 的核心思想就是通过门控机制灵活控制信息的流动,使得模型能够有效学习和处理长时间依赖的任务。
完整案例
我们将基于气象数据来预测未来的气温(或其他气候指标)。
主要步骤如下:
数据准备:从气象历史数据中提取相关的气候变量,如温度、湿度、风速等。 数据预处理:对时间序列数据进行归一化处理,将数据划分为训练集、验证集和测试集。 LSTM模型构建:使用 PyTorch 实现 LSTM 模型进行气候预测。 训练模型:对 LSTM 模型进行训练,并绘制损失曲线和预测结果。 评估和可视化:对模型进行评估,绘制多种图形分析数据和模型效果。
1. 数据准备
首先,我们使用假定的气象数据集(或你可以使用一个真实的气象数据集),例如包含温度、湿度、风速等信息的数据集。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
# 生成假设气象数据集
data_length = 1000 # 假设我们有1000个时间步的数据
np.random.seed(42)
# 生成模拟气象数据(温度、湿度、风速)
dates = pd.date_range(start='1/1/2010', periods=data_length)
temperature = np.sin(np.linspace(0, 20, data_length)) + np.random.normal(0, 0.5, data_length)
humidity = np.cos(np.linspace(0, 15, data_length)) + np.random.normal(0, 0.3, data_length)
windspeed = np.random.normal(3, 1, data_length)
# 创建DataFrame
df = pd.DataFrame({
'Date': dates,
'Temperature': temperature,
'Humidity': humidity,
'WindSpeed': windspeed
})
# 设置日期为索引
df.set_index('Date', inplace=True)
# 打印数据集
print(df.head())
Date: 时间序列,代表每一个时间步。 Temperature: 气温数据,模拟为正弦波加噪声,模拟不同时间的气温变化。 Humidity: 湿度数据,模拟为余弦波加噪声。 WindSpeed: 风速数据,生成为正态分布的随机数。
通过这些数据进行预测,即通过一段时间的气候信息预测未来的气温。
2. 数据预处理
在LSTM模型中,需要对数据进行归一化,并构造训练集和测试集。归一化的目的是将所有数据缩放到相同的范围内,便于模型的收敛。
# 数据归一化
scaler = MinMaxScaler(feature_range=(-1, 1))
scaled_data = scaler.fit_transform(df)
# 构造序列数据
def create_sequences(data, seq_length):
xs, ys = [], []
for i in range(len(data) - seq_length):
x = data[i:i+seq_length]
y = data[i+seq_length, 0] # 预测温度
xs.append(x)
ys.append(y)
return np.array(xs), np.array(ys)
seq_length = 50 # 设定时间序列长度
X, y = create_sequences(scaled_data, seq_length)
# 划分训练集和测试集
train_size = int(0.8 * len(X))
X_train, X_test = X[:train_size], X[train_size:]
y_train, y_test = y[:train_size], y[train_size:]
# 转换为PyTorch张量
X_train = torch.from_numpy(X_train).float()
X_test = torch.from_numpy(X_test).float()
y_train = torch.from_numpy(y_train).float()
y_test = torch.from_numpy(y_test).float()
归一化:将所有数据缩放到[-1, 1]范围。 序列化:将连续的气象数据分割成长度为的序列。 划分数据集:80%的数据作为训练集,20%的数据作为测试集。
3. 构建LSTM模型
使用 PyTorch 来构建一个简单的 LSTM 模型,输入为过去一段时间的气象数据,输出为预测的未来气温。
class LSTM(nn.Module):
def __init__(self, input_size=3, hidden_layer_size=100, output_size=1):
super(LSTM, self).__init__()
self.hidden_layer_size = hidden_layer_size
self.lstm = nn.LSTM(input_size, hidden_layer_size)
self.linear = nn.Linear(hidden_layer_size, output_size)
self.hidden_cell = (torch.zeros(1, 1, self.hidden_layer_size),
torch.zeros(1, 1, self.hidden_layer_size))
def forward(self, input_seq):
lstm_out, self.hidden_cell = self.lstm(input_seq.view(len(input_seq), 1, -1), self.hidden_cell)
predictions = self.linear(lstm_out.view(len(input_seq), -1))
return predictions[-1]
# 实例化模型
model = LSTM()
# 定义损失函数和优化器
loss_function = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
# 训练LSTM模型
epochs = 150
for epoch in range(epochs):
for i in range(len(X_train)):
model.hidden_cell = (torch.zeros(1, 1, model.hidden_layer_size),
torch.zeros(1, 1, model.hidden_layer_size))
# 清空梯度
optimizer.zero_grad()
# 计算输出
y_pred = model(X_train[i])
# 计算损失
single_loss = loss_function(y_pred, y_train[i].view(1))
single_loss.backward() # 反向传播
optimizer.step() # 更新权重
if epoch % 10 == 0:
print(f'Epoch {epoch} Loss: {single_loss.item()}')
print(f'Final Loss: {single_loss.item()}')
输入层:输入过去50天的气象数据,每个输入包含3个变量(温度、湿度、风速)。 LSTM层:LSTM隐含层,包含100个隐藏单元。 全连接层:LSTM层的输出经过线性层转化为预测值。
4. 模型评估和可视化
在模型训练完成后,我们使用测试数据来评估模型的表现。
# 模型预测
model.eval()
test_predictions = []
for i in range(len(X_test)):
with torch.no_grad():
model.hidden_cell = (torch.zeros(1, 1, model.hidden_layer_size),
torch.zeros(1, 1, model.hidden_layer_size))
y_test_pred = model(X_test[i])
test_predictions.append(y_test_pred.item())
# 仅对温度列进行逆归一化
# 获取scaler的参数
scaler_temp = MinMaxScaler(feature_range=(-1, 1))
scaler_temp.min_ = scaler.min_[0]
scaler_temp.scale_ = scaler.scale_[0]
# 对测试集的预测结果进行逆归一化
true_predictions = scaler_temp.inverse_transform(np.array(test_predictions).reshape(-1, 1))
# 对真实温度值进行逆归一化
y_test_true = scaler_temp.inverse_transform(y_test.numpy().reshape(-1, 1))
# 绘制预测结果与真实值的对比
plt.figure(figsize=(12,6))
plt.plot(df.index[-len(y_test_true):], y_test_true, label='True Temperature', color='blue')
plt.plot(df.index[-len(y_test_true):], true_predictions, label='Predicted Temperature', color='red')
plt.xlabel('Date')
plt.ylabel('Temperature')
plt.title('Temperature Prediction vs True Temperature')
plt.legend()
plt.show()
# 绘制损失曲线
losses = []
model.train()
for epoch in range(epochs):
for i in range(len(X_train)):
optimizer.zero_grad()
y_pred = model(X_train[i])
single_loss = loss_function(y_pred, y_train[i].view(1))
single_loss.backward()
optimizer.step()
if epoch % 10 == 0:
losses.append(single_loss.item())
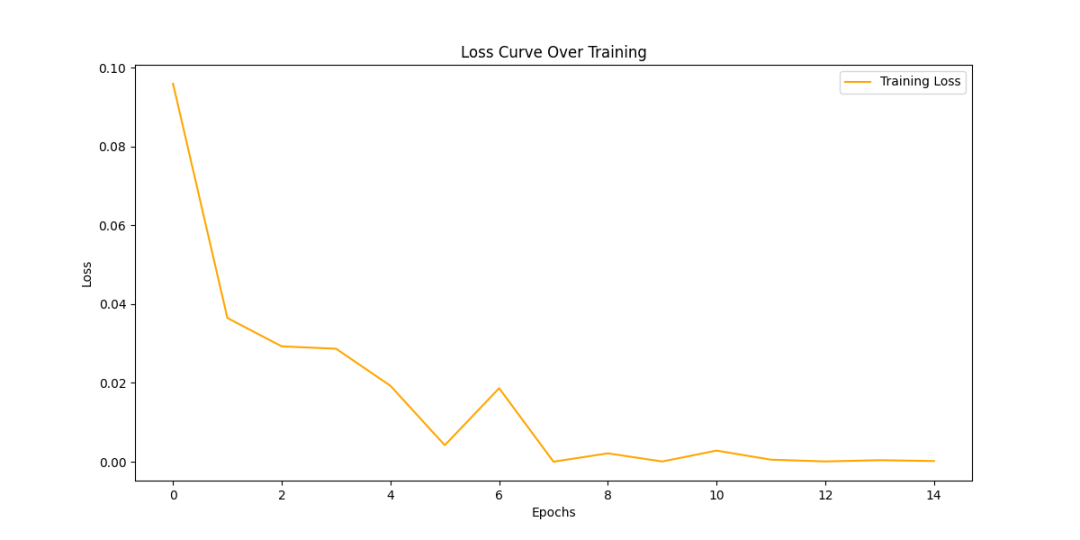
plt.figure(figsize=(12,6))
plt.plot(losses, label='Training Loss', color='orange')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Loss Curve Over Training')
plt.legend()
plt.show()
# 绘制温度时间序列图
plt.figure(figsize=(12,6))
plt.plot(df.index, df['Temperature'], label='Temperature', color='green')
plt.xlabel('Date')
plt.ylabel('Temperature')
plt.title('Historical Temperature Data')
plt.legend()
plt.show()
# 绘制其他气候因素(湿度、风速)随时间变化的趋势图
plt.figure(figsize=(12,6))
plt.plot(df.index, df['Humidity'], label='Humidity', color='purple')
plt.plot(df.index, df['WindSpeed'], label='WindSpeed', color='cyan')
plt.xlabel('Date')
plt.ylabel('Value')
plt.title('Humidity and WindSpeed Over Time')
plt.legend()
plt.show()
预测结果与真实值对比图:模型预测的气温与真实气温的对比,红色线为预测结果,蓝色线为真实值。

损失曲线:展示了模型训练过程中损失值的变化趋势,随着训练迭代次数增加,损失值逐渐减小,说明模型逐渐学习到数据规律。
温度时间序列图:展示了整个时间段内的气温变化情况,帮助理解数据的整体趋势。

湿度和风速随时间变化图:展示了湿度和风速的变化趋势,有助于观察其他气候变量的波动情况。
