哈喽,大家好~
今天和大家聊聊贝叶斯回归,把原理和案例都详细的给大家进行一个介绍~
首先,“回归”就是找规律,用一个公式把输入和输出联系起来。
比如:
输入:房子的面积 输出:房子的价格
普通的线性回归就是假设:
房价 ≈ 截距 + 面积 × 单价
然后用数据(很多房子的面积和价格)来算出“单价”和“截距”。
贝叶斯回归和普通回归的区别
普通回归:
算出来一个固定的“单价”和“截距”。 就像告诉你:每平米 3000 元,固定了。
贝叶斯回归:
它会告诉你“单价”不是一个死数,而是一个分布。 比如,它会说:“单价大概率在 2800~3200 之间,最可能是 3000。”
也就是说,贝叶斯回归会把不确定性算进去。
贝叶斯的核心一句话:后验 ∝ 似然 × 先验
先验:我原来的信念(没看数据之前的猜测)。
比如,我觉得北京郊区的房子单价大概 3000 元/平米,但我不是很确定,可能浮动 ±500 元。
似然:数据能告诉我的信息。
我去收集了 10 套房子的数据(面积和价格)。
后验:结合“先验”和“数据”,得出的新结论。
数据会修正我的原始想法,最后得到更靠谱的“单价分布”。
举个例子:假设你要猜老师的身高。
先验(经验):你觉得老师大概 175cm 左右,但可能在 170~180cm 之间。
收集数据:你偷偷量了老师的桌子高度、和学生合照里的比例……(这些数据可能有点噪声)。
似然:数据告诉你:“看起来老师可能比 170cm 高一点”。
后验:把先验和数据结合起来,你的最终结论可能是:
老师的身高最可能在 174~176cm 之间 95% 的概率在 172~178cm 之间
这就是贝叶斯回归在做的事。它不是给你一个死板的“老师 175cm”,而是给你一个身高分布,让你知道结论的不确定性。
核心原理
模型假设
线性回归模型:
是目标变量 是特征向量 是权重参数 噪声 为高斯分布
似然函数
给定 个样本:
先验分布
假设权重服从零均值高斯先验:
为先验精度(precision)
后验分布
贝叶斯公式:
因为都是高斯分布,后验也是高斯:
其中:
预测分布
对于新样本 :
均值预测: 不确定性(方差):
案例实现
我们生成一个非线性关系的数据集,并用贝叶斯线性回归拟合~
数据分布图 后验权重分布 预测曲线与不确定性 残差分析图
import numpy as np
import matplotlib.pyplot as plt
# 1. 数据集
np.random.seed(42)
N = 500
X = np.linspace(-3, 3, N)[:, None] # (N,1)
y_true = 0.5 * X**3 - X + 2
y = y_true + np.random.normal(0, 5, size=(N,1))
# 添加多项式特征(x, x^2, x^3)
X_poly = np.hstack([X, X**2, X**3])
# 2. 贝叶斯回归公式实现
alpha = 2.0 # 权重先验精度
sigma2 = 3.0**2 # 噪声方差
# 计算后验协方差和均值
S_N_inv = alpha * np.eye(X_poly.shape[1]) + (1/sigma2) * X_poly.T @ X_poly
S_N = np.linalg.inv(S_N_inv)
m_N = (1/sigma2) * S_N @ X_poly.T @ y
# 3. 预测新数据
X_test = np.linspace(-4, 4, 200)[:, None]
X_test_poly = np.hstack([X_test, X_test**2, X_test**3])
y_pred_mean = X_test_poly @ m_N
y_pred_var = np.sum(X_test_poly @ S_N * X_test_poly, axis=1) + sigma2
y_pred_std = np.sqrt(y_pred_var)
# 4. 可视化分析
plt.figure(figsize=(16,12))
# 图1:原始数据与真实曲线
plt.subplot(2,2,1)
plt.scatter(X, y, c='magenta', label='Noisy data')
plt.plot(X_test, 0.5*X_test**3 - X_test + 2, 'b--', label='True function')
plt.title("Original Data vs True Function")
plt.legend()
# 图2:后验权重分布(使用简单可视化)
plt.subplot(2,2,2)
for i in range(len(m_N)):
plt.bar(i, m_N[i,0], yerr=np.sqrt(np.diag(S_N))[i], color='cyan', alpha=0.7)
plt.title("Posterior Distribution of Weights")
plt.xlabel("Weight index")
plt.ylabel("Value")
# 图3:预测曲线与不确定性
plt.subplot(2,2,3)
plt.plot(X_test, y_pred_mean, 'green', label='Predictive mean')
plt.fill_between(X_test.flatten(),
y_pred_mean.flatten()-2*y_pred_std,
y_pred_mean.flatten()+2*y_pred_std,
color='yellow', alpha=0.3, label='Uncertainty (±2σ)')
plt.scatter(X, y, c='red', label='Data')
plt.title("Predictive Mean and Uncertainty")
plt.legend()
# 图4:残差分析
plt.subplot(2,2,4)
residuals = y.flatten() - (X_poly @ m_N).flatten()
plt.scatter(X.flatten(), residuals, c='orange')
plt.hlines(0, X.min(), X.max(), colors='black', linestyles='dashed')
plt.title("Residual Analysis")
plt.xlabel("X")
plt.ylabel("Residuals")
plt.tight_layout()
plt.show()
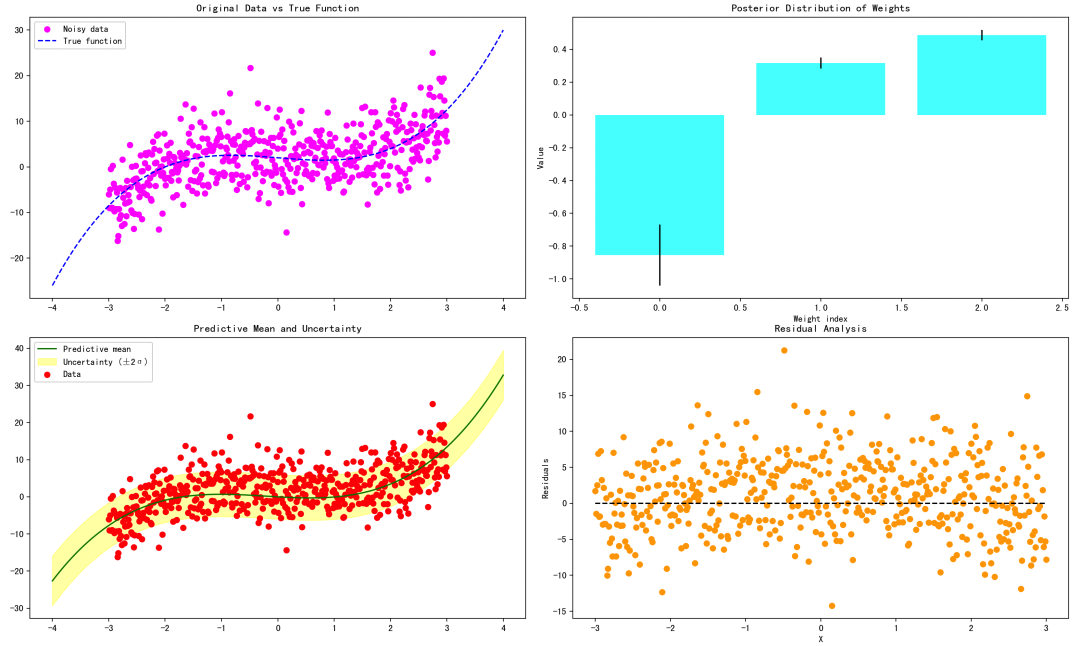
原始数据 vs 真值曲线:展示生成数据的噪声和真实函数,便于观察噪声影响。 后验权重分布:显示贝叶斯回归得到的权重均值与不确定性(标准差),可以看出哪些多项式项贡献大。 预测曲线与不确定性:预测曲线(均值)和置信区间(±2σ),显示模型对未知点的不确定性。 残差分析:分析预测与真实观测的差距,检验模型是否存在系统偏差。
整个案例体现了贝叶斯线性回归的核心思想,包括后验分布、预测分布和不确定性分析,大家可以结合理论和注释,逐步学习~
最后

