编辑:冷猫
早在 2021 年,研究人员就已经发现了深度神经网络常常表现出一种令人困惑的现象,模型在早期训练阶段对训练数据的记忆能力较弱,但随着持续训练,在某一个时间点,会突然从记忆转向强泛化。
类似于「顿悟时刻」,模型在某一刻突然理解了数据的内在规律。
这种现象被称为「grokking(延迟泛化)」。该现象挑战了传统关于过拟合与泛化关系的理解,因此成为揭示神经网络学习机制的重要研究方向。

数年时间过去,相信大家对大模型的「顿悟时刻」早已不陌生,在探究大模型 grokking 的成因和基本原理的领域已经有了许多重量级研究。
我们也曾经报道过;等相关内容。
而在最近, Meta 超级智能实验室(FAIR)的新论文再一次针对顿悟现象进行了更深层次的探讨,这篇论文通过给出 grokking 现象的数学可解释模型,让人们更清楚地理解深度网络如何从「死记硬背」过渡到「真正学习」。
值得关注的是,这篇文章仅有唯一作者:Meta FAIR 研究科学家总监田渊栋,是一篇一个人的论文。

论文标题:Provable Scaling Laws of Feature Emergence from Learning Dynamics of Grokking
论文链接:arxiv.org/abs/2509.21519

本研究提出了一个名为 Li₂ 的数学框架,用以解释 Grokking(延迟泛化) 现象在两层非线性神经网络中的学习动态。具体来说,该框架:
精确描述了训练过程中将会涌现的特征,揭示了模型如何逐步形成泛化表示;
给出了泛化与记忆的可证明缩放定律 —— 对于阶数为 M 的群运算任务,仅需 O (M log M) 个数据样本即可实现泛化行为;
从理论上解释了一个流行经验假设:即「泛化电路学习速度较慢,但比记忆电路更高效」。

Li₂ 框架概览。
如图所示,Li₂ 将学习过程划分为三个阶段 ——(I) 惰性学习(Lazy learning)、(II) 独立特征学习(Independent feature learning)以及 (III) 交互特征学习(Interactive feature learning),以此解释 grokking 的动力学过程,即网络先经历「记忆」阶段后再实现「泛化」。
Grokking 行为的解释:在 grokking 初期,惰性学习阶段对应记忆过程,顶层利用随机特征找到一个暂时的解来拟合目标。之后,反向传播的梯度才开始有意义,促使隐藏层学习到可泛化的「新兴特征」。
新兴特征:这些特征是能量函数 E 的局部极大值,支配着独立学习阶段。这些特征在标签预测上的效率高于简单记忆。
数据决定能量景观:充足的训练数据可以保持这些可泛化局部极大值的形状,而数据不足则会导致非泛化的局部极大值。
特征出现、泛化与记忆的尺度律:通过研究能量景观随数据分布变化的方式,可以推导出相应的尺度规律。
如图右侧所示,论文分析覆盖了不同的网络宽度 K 和权重衰减系数 η,展示了它们对学习动态的影响,涵盖 NTK 区域与特征学习区域。在特征学习阶段,借助能量函数 E(定理 1),我们将学习到的特征描述为 E 的局部极大值(定理 2),并推导出维持这些特征所需的样本规模,从而建立了泛化与记忆的尺度律。

Li₂ 框架的三个阶段 (a) 随机权重初始化。(b) 阶段 I:惰性学习。(c) 阶段 II:独立特征学习。 (d) 阶段 III:交互特征学习。
阶段 I:惰性学习
在这一初始阶段,输出层权重 V 会迅速调整,以随机初始化的隐藏特征来拟合训练数据。反向传播到隐藏层的梯度 G_F 基本上仍是随机噪声,无法驱动隐藏层权重 W 学到有意义的特征。这导致模型表现为「记忆」行为,泛化能力较差。

实验验证结果展示了 grokking 的三个阶段:在 输出层发生过拟合(阶段 I) 之后,隐藏层权重才开始更新。
阶段 II:独立特征学习
当权重衰减项 (η> 0) 生效时,梯度 G_F 开始携带关于目标标签的结构化信息,模型进入第二阶段。论文证明,在一定条件下,每个隐藏单元的动态是相互独立的,并遵循以下能量函数的梯度上升过程(定理 1):
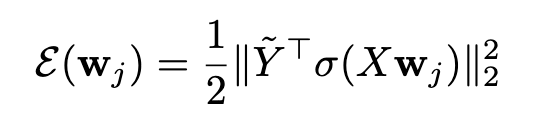
该能量函数可视为输入与目标之间的一种非线性典型相关分析(nonlinear CCA)。

能量函数 E 的景观变化
左图:当采用线性激活时,E 可简化为普通的特征分解,仅存在一个全局最大值。
中图:引入非线性后,能量景观出现多个严格的局部最大值,每个最大值对应一个特征。更重要的是,这些特征在目标预测中比记忆化更高效。
右图:当训练数据充足时,能量景观保持稳定,可以恢复这些具有泛化能力的特征;而当数据不足时,能量景观会发生显著变化,局部最大值退化为记忆化特征。

模加任务中的泛化 / 记忆相变
实验表明:随着群结构复杂度增加(特别是非阿贝尔群),泛化阈值的变化依然符合理论的对数尺度规律,验证了 Li₂ 框架推导的特征涌现与泛化的尺度定律(scaling law)。

在模加运算的小数据场景下,设 M = 127 且 n = 3225(在 1272 个样本中使用 20% 进行训练),使用较小学习率的 Adam 优化器(0.001,对应左图;0.002,对应中图)能够得到可泛化的解(傅里叶基),并且误差 E 较低;而当使用较大学习率(0.005,对应右图)时,Adam 则会找到不可泛化的解(例如记忆化),此时误差 E 明显更高。
群算术任务相关内容,请参阅原论文。
阶段 III:交互特征学习
随着隐藏层权重不断更新、特征逐渐涌现,隐藏单元之间的交互开始变得显著。该框架表明,相似特征之间会产生「排斥效应」,而梯度结构则会自适应地优先学习尚未捕获的特征,从而保证特征表示的多样性与完整性。
我们首先研究 B 的作用,它会引起隐藏节点之间的相互作用。在训练过程中,两个节点的激活可能高度相关,定理 6 表明,相似的特征会导致排斥效应。

在训练过程中,某些局部最优解可能先被学习,而其他则在后期才被学习。当表示仅被部分学习时,反向传播提供了一种机制,可以聚焦于尚未学习的部分,通过改变能量函数 E 的形态来实现(定理 7,自上而下的调制)。
对于具有 Σ(x) = x^2 的群算术任务,如果隐藏层仅学习了一部分不可约表示集合 S,那么反向传播梯度
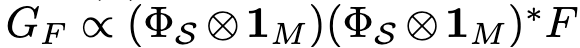
会产生一个修改后的能量函数 E_S,其局部最大值仅出现在尚未学习的不可约表示 k∉S 上。
对更深网络的扩展
虽然严格分析集中在两层网络上,论文也给出了对更深架构的定性扩展。核心观点是,特征学习会从低层向高层传播,而残差连接(residual connections)可能提供更干净的梯度,从而促进多层特征的生成。

Adam 与 Muon 优化器的比较结果表明,Muon 在实现泛化方面表现更优,尤其是在隐藏单元数量受限的情况下。
总结与讨论
两种不同的记忆(memorization)类型
从分析来看,grokking 中的记忆来源于对随机特征的过拟合,这与由于有限或噪声数据而遵循特征学习动力学得到的记忆解不同。从这个角度看,grokking 并不是从记忆切换到泛化,而是从过拟合切换到泛化。
平坦(flat)与尖锐(sharp)极值
常识通常认为平坦极值对应可泛化解,而尖锐极值对应记忆或过拟合。从 Li₂ 的观点来看,当模型对随机特征过拟合时会出现尖锐极值,此时权重的微小变化会导致损失大幅变化。另一方面,我们可以证明能量函数 E 的局部极值是平坦的,因此在某些方向上权重的小幅变化不会改变 E。如果模型是过参数化的,则多个节点可能学习相同或相似的特征集合,从而为损失函数提供平坦性。如果由于有限 / 噪声数据学习了记忆特征,则需要更多节点参与「解释」目标,整体权重会显得不那么平坦。
小学习率与大学习率
根据分析,在阶段 I,需要较大学习率以快速学习脊状解 V,使反向传播梯度 G_F 变得有意义,从而触发阶段 II。在阶段 II,最佳学习率取决于可用数据量:
数据量大时,可以使用较大学习率快速找到特征。
数据量有限时,可能需要较小学习率以保持在可泛化特征的盆地内,这可能与常识认知相矛盾。
更多研究细节,请参阅原论文。

© THE END
转载请联系本公众号获得授权
投稿或寻求报道:liyazhou@jiqizhixin.com










