哈喽,大家好~
今儿和大家聊聊深度学习中非常常用的一个优化器,Adam。
Adam优化器(Adaptive Moment Estimation)是一种用于训练深度学习模型的梯度优化算法。它结合了动量法(Momentum)和RMSProp算法的优点,能够以自适应的方式调整每个参数的学习率,从而加快模型的训练速度并提高收敛的稳定性。Adam通过维护梯度的一阶动量(平均值)和二阶动量(梯度平方的指数加权移动平均值)来动态调整学习率,使得在不同维度上能够进行更精细的学习。
直白点讲,Adam优化器可以理解为一种“聪明的调参助手”,它能帮助你的模型更高效地学习。
假设在爬一座山(优化目标),Adam相当于给你提供了两个工具:
记住你最近的动作方向(梯度):Adam会追踪你之前爬的方向,比如你连续几次向东南方向爬,那它会认为东南可能是个好方向,就会加快这个方向的步伐(动量)。 注意地形的变化:Adam还会观察地形,如果你前面走的地方坡度特别陡,它会帮你小心一点,走得慢一些;而在相对平坦的地方,它会鼓励你迈大步(自适应学习率)。
这样,Adam可以帮你快速找到最优解(山顶),不用总是原地打转或者走得太快掉下去。它的“自适应”特性让每一步的调整都更为智能化,能够适应不同的地形(模型的不同参数)来进行更好的调整。
总结来说,Adam的好处就是它既能记住走的方向,又能根据当前的地形变化动态调整步伐,从而让模型的训练更加稳定和高效。
理论基础
Adam优化器是一种结合了动量法(Momentum)和RMSProp的自适应学习率优化算法,它利用梯度的一阶和二阶动量(均值和方差)来调整每个参数的学习率,确保在不同维度上学习步伐的智能化调整。
1. 初始化参数
在训练开始时,我们需要初始化一些超参数以及模型的权重:
学习率 (通常默认值为 )
一阶动量衰减因子 (通常默认值为 )
二阶动量衰减因子 (通常默认值为 )
防止除零的小常数 (通常默认值为 )
初始化参数 (即模型的权重)
初始化一阶动量估计
初始化二阶动量估计
2. 计算梯度
在每次迭代的步骤 ,我们会基于当前模型的损失函数 计算出每个参数 的梯度:
这个梯度 表示了损失函数对参数的变化率,指示了参数如何更新才能最小化损失。
3. 更新一阶动量估计(动量法)
一阶动量估计是梯度的指数加权移动平均(指数平滑的均值),类似于“动量”的概念。动量法的目的是让梯度在历史上的变化方向产生影响,以便能在梯度更新过程中加速。
更新公式为:
其中:
是动量衰减因子,控制着历史梯度的影响大小,值越接近1,表示历史梯度的影响越大。 是当前时刻的动量估计,表示梯度的指数加权平均。
4. 更新二阶动量估计(RMSProp 部分)
二阶动量估计是梯度平方的指数加权移动平均,用来衡量梯度的方差。它类似于RMSProp算法中的梯度平方的平滑,这有助于动态调整学习率。
更新公式为:
其中:
控制二阶动量的衰减速度,值越接近1,表示对历史平方梯度的考虑越多。 是当前时刻的二阶动量估计,表示梯度平方的指数加权平均。
5. 偏差校正
由于在动量和均方根估计的计算中采用了指数加权平均,在初期迭代时, 和 的值会偏小,导致优化器的更新效果不准确。因此,Adam引入了偏差校正,使得初始时刻的估计更加准确。
偏差校正公式为:
其中 和 分别是偏差校正后的动量和均方根估计。这一步的目的是让初始动量和方差的估计值更加准确。
6. 更新参数
参数 的更新公式结合了偏差校正后的动量和二阶动量估计。通过动态调整学习率,Adam能够在不同维度上以不同的速度进行更新,保证每个参数都有合适的步伐。
更新公式为:
其中:
是全局学习率,它决定了参数更新步伐的大小。 是偏差校正后的动量,用来表示当前更新的方向。 是偏差校正后的均方根,用来调节每个参数更新时的步伐。 是一个小数,用于防止分母出现零或接近零的情况。
7. 循环迭代
上述步骤重复执行,直到达到预定的训练终止条件(如达到最大迭代次数或损失函数收敛)。Adam会不断地在每个迭代中调整参数,直至模型训练完成。
8. 总结
Adam的整个流程可以总结为以下步骤:
初始化参数 、一阶动量 和二阶动量 ,设定超参数 、、、。 在每个时刻 :
计算当前梯度 。 更新一阶动量 。 更新二阶动量 。 进行偏差校正 、。 使用校正后的动量和均方根更新参数 。
9. Adam的特点与优点
自适应学习率:每个参数都有独立的学习率,可以根据不同维度的梯度调整学习步伐。 结合动量与RMSProp的优势:动量法加速梯度下降,RMSProp通过平方梯度平滑避免过大的梯度。 稳定性:偏差校正机制使得初始阶段的更新更加准确,防止算法收敛过慢或过快。 适用于稀疏梯度问题:Adam在处理稀疏梯度的优化问题上表现优异。
通过以上详细步骤,Adam可以稳定且高效地进行模型训练,是深度学习中非常常用的优化算法之一。
应用场景
Adam优化器适用于以下几类问题:
深度学习模型的训练:它常用于深度神经网络的优化,尤其是在处理大规模、高维数据集时表现出色。 稀疏梯度问题:例如自然语言处理(NLP)中的词嵌入,图像处理中的稀疏特征提取等,Adam能有效处理这种梯度更新不频繁的情况。 非平稳目标函数:目标函数会随着时间或训练进展而变化时(如强化学习中的值函数优化),Adam可以动态调整学习率,帮助模型更好地适应变化。
Adam优化器的优缺点
优点:
自适应学习率:Adam对每个参数都有独立的自适应学习率调整,使得模型训练更加灵活和高效,减少了手动调节学习率的工作。 快速收敛:结合动量法与RMSProp的优势,Adam能够加快收敛速度,尤其是在面对稀疏梯度或不规则梯度变化时。 稳健性强:偏差校正机制提高了训练初期的稳定性,防止收敛过快或陷入局部最优。 适合大规模数据和网络:在处理大规模数据集和深度神经网络时表现优秀,不需要额外的调整就能取得较好效果。
缺点:
可能过拟合:由于Adam的适应性强,它可能在某些任务上表现过于灵活,容易陷入局部最优或过拟合,尤其是在数据较小或噪声较大时。 有时收敛不充分:尽管Adam收敛较快,但在某些场景下,尤其是收敛到较小学习率时,它可能无法进一步优化到全局最优解。 对超参数较为敏感:尽管Adam默认的超参数表现通常不错,但在一些特定任务上,学习率、动量衰减等超参数可能需要仔细调节。
Adam优化器的运用前提条件
深度学习任务:适用于深度神经网络的优化,尤其是大规模数据集或复杂神经网络结构(如卷积神经网络、循环神经网络)。 数据规模较大:Adam在处理大规模、高维数据集时有较好的表现。 梯度稀疏性:当模型的梯度更新不频繁(如NLP中的词嵌入、稀疏特征学习)时,Adam的自适应学习率机制能更好地应对。 目标函数变化较大:适用于不平稳的优化问题,如强化学习中的动态目标。
实际中的应用案例
自然语言处理(NLP):在训练词嵌入模型(Word2Vec、GloVe)时,Adam常用来优化稀疏的词向量表示。由于自然语言处理中的梯度往往稀疏,Adam的自适应学习率能够更有效地处理这种情况。
计算机视觉:在卷积神经网络(CNN)的训练中,Adam被广泛用于图像分类、物体检测等任务,尤其是在处理大规模的图像数据集(如ImageNet)时表现优异。Adam的快速收敛特性让训练大规模网络的时间显著减少。
强化学习(Reinforcement Learning):在强化学习中,Adam常用于优化值函数(Value Function)或策略网络。因为强化学习的目标函数往往不平稳,Adam的自适应性可以帮助模型适应目标函数的变化,提升模型的表现。
生成对抗网络(GAN):在训练生成对抗网络(GAN)时,Adam优化器通常用来更新生成器和判别器的参数。GAN的损失函数通常不稳定且梯度变化较大,Adam可以有效缓解训练过程中的不稳定性,加速收敛。
Adam优化器是深度学习中非常重要且常用的优化算法,适用于稀疏梯度、非平稳目标函数以及大规模神经网络等场景。通过自适应学习率的机制,它能够提升训练效率,并在多种任务上表现出色。
完整案例
这里咱们使用PyTorch和虚拟数据集的完整实现,结合了Adam优化器来训练一个简单的神经网络进行回归任务,最后通过绘制多个图形展示训练过程和结果。
包括:
生成虚拟数据集。 使用PyTorch构建神经网络模型,并使用Adam优化器进行训练。 可视化包括训练过程中的损失曲线和模型预测结果与实际值的对比。
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# 生成虚拟回归数据集
X, y = make_regression(n_samples=2000, n_features=10, noise=0.1)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 将数据转为tensor格式
X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32).view(-1, 1)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.float32).view(-1, 1)
# 标准化数据
scaler = StandardScaler()
X_train = torch.tensor(scaler.fit_transform(X_train), dtype=torch.float32)
X_test = torch.tensor(scaler.transform(X_test), dtype=torch.float32)
# 构建神经网络模型
class NeuralNet(nn.Module):
def __init__(self):
super(NeuralNet, self).__init__()
self.fc1 = nn.Linear(X_train.shape[1], 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 1)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = self.fc3(x)
return x
model = NeuralNet()
# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
# 训练模型
epochs = 200
train_losses = []
test_losses = []
for epoch in range(epochs):
model.train()
optimizer.zero_grad()
outputs = model(X_train)
loss = criterion(outputs, y_train)
loss.backward()
optimizer.step()
train_losses.append(loss.item())
# 计算测试集上的损失
model.eval()
with torch.no_grad():
test_outputs = model(X_test)
test_loss = criterion(test_outputs, y_test)
test_losses.append(test_loss.item())
# 绘制图像
plt.figure(figsize=(14, 7))
# 图1:训练和测试损失随epoch的变化
plt.subplot(1, 2, 1)
epochs_range = range(1, epochs + 1)
plt.plot(epochs_range, train_losses, label='Training Loss', color='blue', linewidth=3)
plt.plot(epochs_range, test_losses, label='Testing Loss', color='red', linestyle='--', linewidth=3)
plt.fill_between(epochs_range, train_losses, test_losses, color='', alpha=0.1)
plt.title('Training vs Testing Loss', fontsize=14)
plt.xlabel('Epochs', fontsize=12)
plt.ylabel('Loss', fontsize=12)
plt.legend()
plt.grid(True)
# 图2:预测值与真实值的对比
plt.subplot(1, 2, 2)
with torch.no_grad():
y_pred = model(X_test).numpy()
y_test_np = y_test.numpy()
plt.scatter(y_test_np, y_pred, label='Predicted vs Actual', color='green', s=40, alpha=0.7)
plt.plot([min(y_test_np), max(y_test_np)], [min(y_test_np), max(y_test_np)], color='orange', linestyle='--', linewidth=3)
plt.title('Predicted vs Actual Values', fontsize=14)
plt.xlabel('Actual Values', fontsize=12)
plt.ylabel('Predicted Values', fontsize=12)
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
数据生成:使用
make_regression函数生成了一个包含 1000 个样本、10 个特征的虚拟回归数据集。数据集通过train_test_split切分为训练集和测试集,并标准化处理。神经网络模型:构建了一个包含 2 个隐藏层(64个神经元)的神经网络,并使用 ReLU 激活函数。最后一层输出 1 个值(回归任务)。
Adam优化器:使用 PyTorch 内置的 Adam 优化器进行模型训练,学习率为 0.001。
训练过程:在 200 个迭代中,模型使用训练集进行训练,并在每次迭代中计算训练损失和测试损失。损失函数使用均方误差(MSE)。
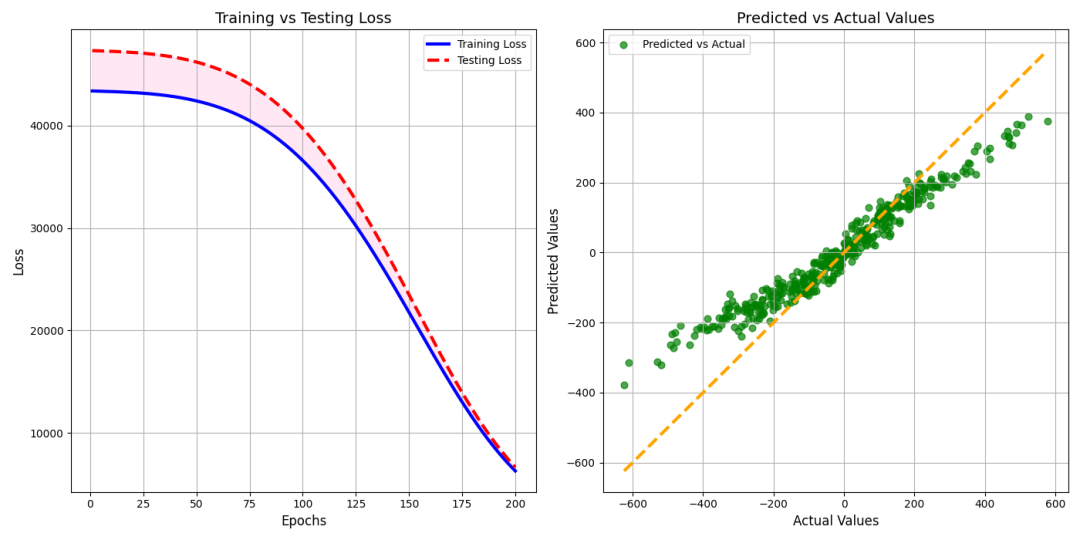
图1:展示训练损失和测试损失随epoch的变化情况,反映模型的学习过程和泛化能力,清晰展示训练过程和预测效果,损失随训练的逐步下降。 图2:展示模型在测试集上的预测值与真实值的对比,分析模型的拟合效果。
最后

