论文题目：FREDF: LEARNING TO FORECAST IN THE FREQUENCY DOMAIN

论文地址：https://arxiv.org/pdf/2402.02399

代码： https://github.com/Master-PLC/FreDF

创新点

• FreDF通过将预测任务从时间域转换到频率域，有效地绕开了标签序列自相关性带来的复杂性。

• FreDF是首次尝试将频率分析用于改进预测范式本身，特别是针对标签序列的自相关性问题。

• FreDF通过在频率域中进行预测，提供了一种通用的解决方案，能够显著提升多种现有模型的性能，而无需对模型架构进行重大修改。这种通用性使得FreDF具有广泛的应用前景。

方法

本文提出了一种名为Frequency-enhanced Direct Forecast (FreDF)的新方法，旨在解决现有直接预测（Direct Forecast, DF）范式中忽略标签序列自相关性的问题。FreDF通过将预测任务从时间域转移到频率域，利用傅里叶变换将时间序列数据转换为频率域表示，从而有效减少自相关性的影响。在频率域中，数据的表示基于正交基，不同频率成分之间的依赖性显著降低，这使得模型能够更好地对齐预测值和真实值的频率成分。FreDF引入了一个频率域损失函数，通过最小化预测值和真实值在频率域中的差异来优化模型性能。

标签序列自相关性可视化

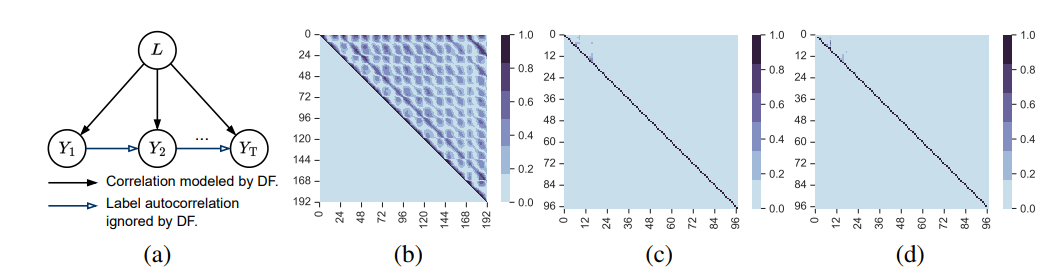
本图展示了时间序列预测中标签序列的自相关性。图 (a) 描述了时间序列数据的生成过程，其中箭头表示时间步之间的依赖关系。图 (b) 使用双重机器学习（DML）方法量化了自相关性，矩阵中的每个元素表示从 Yi 到 Yj 的因果强度。图中对角线元素值为1，表示自相关性；非对角线元素的显著值表明不同时间步之间存在依赖关系，验证了标签序列的自相关性。

频率域依赖性分析

本图展示了频率域中频率成分之间的依赖性。图 (a) 和 (b) 分别展示了频率成分之间依赖性的实部和虚部。通过 DML 方法量化，发现频率成分之间的依赖性显著低于时间域中的自相关性，表明频率域能够有效降低自相关性的影响。

FreDF 方法流程图

本图该图详细展示了 FreDF 方法的工作流程。首先，输入历史序列 L(n)，模型生成多步预测 ˆY (n)。然后，计算时间域中的预测误差 L(tmp)，并将预测值和标签序列转换到频率域，计算频率域中的预测误差 L(feq)。最后，将时间域和频率域的误差融合，形成最终的损失函数 Lα。

实验结果

本表提供了长期预测任务中不同模型的性能对比，展示了FreDF在多个数据集上的显著优势。表中列出了FreDF与其他先进模型（如iTransformer、FreTS、TimesNet等）在ETTm1、ETTm2、ETTh1、ETTh2、ECL、Traffic和Weather等数据集上的平均MSE（均方误差）和MAE（平均绝对误差）。FreDF在多数情况下取得了最低的预测误差，表明其在处理长期预测任务时的有效性和优越性。例如，在ETTm1数据集上，FreDF的MSE为0.392，MAE为0.399，相较于iTransformer的0.415和0.416，FreDF的性能提升明显。这不仅证明了FreDF在减少预测误差方面的有效性，也突显了其在不同数据集和预测长度下的广泛适用性。