OpenAI 最新的推理模型,在与人类选手完全相同的竞赛规则下,成功解决了 2025 年国际数学奥林匹克竞赛中的六道题目中的五道。
这意味着,在攻克全球最顶尖、最艰难的数学挑战上,最聪慧的人类学生与人工智能之间的能力鸿沟,终于被历史性地抹平了。
这一里程碑的到来,比几乎所有领域专家的预言都大大提前。
这个模型并非为数学竞赛专门打造,而是一个通用的大语言模型。
它成功的秘诀在于采用了创新的验证技巧和远超以往的思考时间,从而能够驾驭那些曾让所有机器都束手无策的复杂证明题。
OpenAI 的这次胜利昭示了一个新时代的来临:AI 的能力上限已被重新定义。
通过「验证+智能搜索」的精妙结合,一个现成的通用大语言模型,无需任何领域专属的特殊训练,便能跻身世界顶尖,摘得奖牌。
该模型完整解答了六道题目中的五道,最终取得了 35 / 42 的高分。
在官方为期两天的竞赛规则下,这一成绩已完全达到了人类金牌得主的水准。
在宣布此项成就时,OpenAI 的首席执行官 Sam Altman 也分享了更多信息:
我们很快将发布 GPT-5,但希望能帮助大家建立准确的预期。这是一个实验性的模型(即获得 IMO 金牌的模型),它融合了我们将用于未来核心模型的新研究技术。
我们相信大家会喜爱 GPT-5,但我们并没有计划在未来数月内,发布一款具备同等级别 IMO 金牌解题能力的模型。
奥赛题目要求多页严谨证明,而非单一数字答案
为了攻克这一难题,OpenAI 的团队增设了全新的自我核查机制。
该机制迫使模型必须详细阐述其论证的每一步,并对所有步骤进行交叉检查,以发现任何逻辑上的漏洞。
这一额外的层次,成功地将模糊的推理过程,转变为评分员可以逐行审阅的、严谨的逻辑链条。
模型的思考以小时计,而非秒计
像 o1 这样的早期系统,通常在对问题进行一次快速处理后,便草率地给出完整答案,这无疑会将宝贵的计算资源浪费在错误的路径上。
而全新的架构则将总时间预算,精巧地分解为众多更小规模的搜索任务。
这种策略能够及早识别并放弃没有希望的死胡同,从而将绝大部分算力集中在最有潜力的解题路径上。
国际数学奥林匹克竞赛的提交内容,是极难验证的、长达数页的证明过程。
在此领域取得进展,要求我们必须超越传统强化学习范式中那种对明确、可验证奖励的依赖。
正是通过这一超越,OpenAI 创造出一个能够构建出与顶尖人类数学家相媲美的、复杂且无懈可击的论证能力的模型。
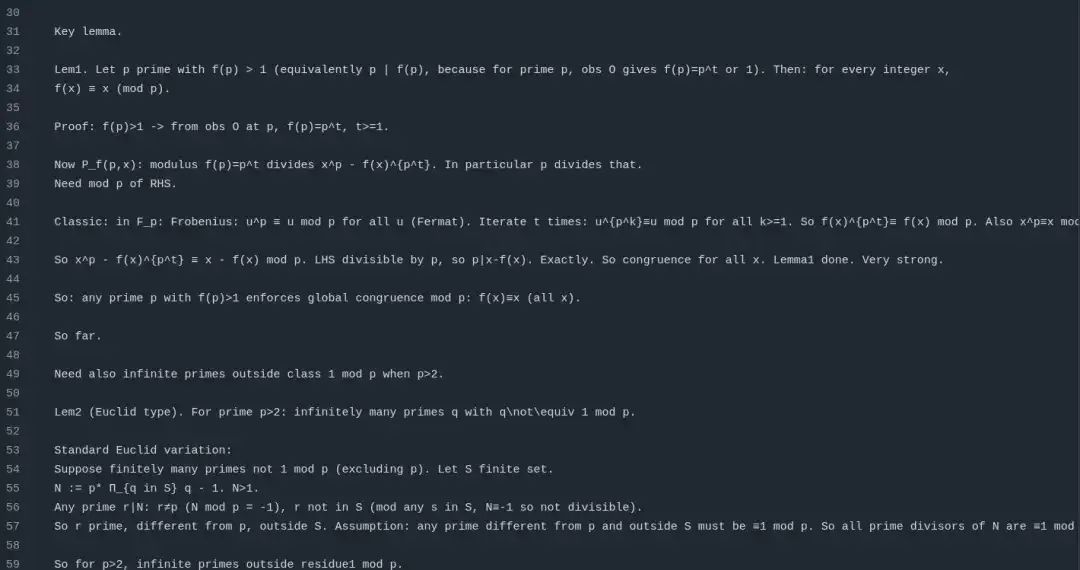
OpenAI 的研究员 Alex 甚至提供了一个 Github 仓库链接,其中包含了该模型解题的完整输出。
评分标准:极致严格
按照国际数学奥林匹克竞赛的官方规则,六道题目每题七分。
该模型凭借完整解答五道题目的优异表现,成功赢得了奖牌。测试期间,不允许使用任何额外数据、计算器或互联网连接。
AI 数学能力的演进:一日千里
回顾 2024 年,各大顶尖实验室仍在以解决 GSM8K(一个小学数学应用题数据集)为荣,以此展示其模型的推理能力。
而到了 2025 年初,美国数学邀请赛级别的难题已变得稀松平常。
在不到两年的时间里,从零到一攻克国际数学奥林匹克竞赛的壁垒,这一巨大的跨越不仅弥合了过往的差距,更预示着类似的推理能力飞跃,可能很快将在其他科学领域上演。
方法论的启示:通用性是关键
值得注意的是,整个训练流程中,没有任何部分是直接针对几何学或数论进行优化的。
其核心策略是训练大语言模型掌握一种通用的解题范式:将任何宏大、困难的目标,拆解为一系列更小、更易于验证的主张,然后逐一核实,并从失败的尝试中学习、迭代。
这一套方法论,可以被平滑地迁移到化学证明、代码正确性验证、乃至物理学推导等多个领域,而无需依赖任何特定领域的定制化插件。
核心洞见:超越规模,拥抱智慧
此役胜利的核心启示在于,单靠模型规模的堆砌已不再是成功的充分条件。
胜利源于更智能的验证策略、更高效的搜索预算分配,以及将复杂问题严谨地转化为模型能够理解的纯文本的能力。
正是这些要素的有机结合,最终推动一个通用大语言模型,突破了一个许多专家曾预测需要数年才能企及的重大基准。
背景解读:赢得 IMO 金牌究竟意味着什么?
想要参加国际数学奥林匹克竞赛,每个国家的代表队都必须经过多轮选拔赛和高强度训练营的层层筛选,其过程之严苛,使得许多国家甚至需要提前数年就开始物色和培养苗子。
能够站上 IMO 的赛场,本身就意味着你已是地球上排名前六百的学生数学解题精英。而最终,他们中只有不到 10%(约 50 人)能够摘得金牌。
竞赛的题目以残酷著称。
这是一场为期两天的智力马拉松,包含两份各 4.5 小时的试卷,每份试卷三道题,每题七分,总分四十二分。
每一道题都经过精心设计,旨在挑战所有已知的标准解题技巧,确保其具备足够的新颖性和证明深度。
在完全相同的时间限制下,且没有任何外部辅助,OpenAI 的最新模型取得了足以斩获这枚珍贵金牌的优异成绩。
这一刻为何重要?
国际数学奥林匹克竞赛的金牌,曾一度被视为大学前数学天赋的最高天花板。
如今,AI 能够与之匹敌,这证明了通用语言模型已经具备了驾驭深度、创造性推理的能力,而不再是过去那种狭隘的数字运算机器。
AI 的进步速度是陡峭的:2024 年,各大实验室还在为解决小学应用题而庆祝;到 2025 年初,模型在处理美国数学邀请赛级别的任务时已显吃力。
在不到二十四个月的时间里,AI 跨越了 IMO 的鸿沟,这强烈预示着,类似的「验证+搜索」复合技巧,可能很快就会席卷化学证明、形式化程序验证和理论物理推导等前沿领域。
模型的规模本身并未带来胜利;关键的突破来自于显式的自我验证机制、更智能的时间预算策略,以及将抽象符号严谨地转化为纯文本的工程纪律。
这个成功的配方,可以被推广到任何一个「逻辑链条」的重要性远超「表面模式匹配」的领域。
近期趋势:大语言模型在数学性能上的高歌猛进
在短短六个月内,一波以自我核查、多智能体和长时程搜索为代表的新兴技术浪潮,让通用大语言模型实现了从解答美国数学邀请赛级别难题到斩获 IMO 金牌的惊人飞跃。
四个月前,o3-Mini 模型在美国数学邀请赛的公开基准测试中,创造了 86.5% 的最佳纪录。
而三天前发布的 Kimi K2,在保持其通用模型定位的同时,已在 MATH-500 数据集上将准确率刷新至 97.4%。
这些连续的突破共同证明:弥合差距的并非是蛮力的规模扩张,而是推理机制本身的革新。
推动大模型数学性能提升的关键研究
自发性自我修正:让单个模型同时扮演两个角色,一个提议者和一个验证者。在 MATH-500 数据集上,该技术仅用一次前向传播,就将 Llama-3.1-70B 的准确率提升了 11.6 个百分点。

思维树采样重访:对经典的搜索方法进行了精简。它不再盲目扩展数千个分支,而是通过一个自适应采样器,仅培育少数能通过轻量级检查的有潜力的分支,在保持同等准确率的同时,将计算量减少了一半。
模型集群:将十几个经过微调的模型视为一个协同工作的集群。在推理时,它们共享中间证明,从而迅速收敛到当前最严谨的论证,在内部测试中,这项技术将奥赛级别难题的得分提高了 8-10 分。
DeepSeek-R1:证明了纯粹的强化学习,无需任何人类标注,就能教会基础模型如何奖励严谨的逐步推理。经过三天的强化学习训练,它在数学和编码任务上的表现已超越了同类有监督模型。
APOLLO:将 Lean-4 证明检查器无缝整合到推理循环中。当生成的证明失败时,APOLLO 只修复错误的那一行,而非从头再来,这在形式化定理任务中将所需的样本数量锐减了 70%。
MA-LoT:通过多个能理解 Lean 语言的智能体进一步扩展了该思想。这些智能体将高层次的自然语言推理与低层次的形式化步骤分离开来,让每个部分各司其职,从而加速了收敛过程。
形式化证明 RAG:该流程会在生成答案之前,先检索相似的、已解决的定理作为参考,然后对新生成的每一步进行验证。这一方法推动了小型模型在今年二月发布的一个新 Lean 证明基准套件上的性能表现。
驱动前沿竞赛的基准测试
Math-RoB (2025 年 3 月):专注于评估模型在处理不完整或误导性输入时的稳健性,这暴露了仅靠准确率测试所无法发现的系统脆弱性。
ReliableMath (2025 年 7 月):通过引入无法解决的陷阱问题,来捕捉模型凭空捏造证明的幻觉行为,从而在准确率之外,提供一个更维度的可靠性评分。
FINE-EVAL (2025 年 5 月):引入了 Lean 填空挑战,使研究人员能够检验模型是真正理解了证明的逻辑,还是仅仅记忆了完整的证明过程。
这些新兴的评估标准,旨在惩罚投机取巧的猜测策略,并奖励上文所述的、那些以严谨验证为核心的先进技术。
总结:我们如今身在何方?
国际数学奥林匹克竞赛,向来是淬炼全球最杰出年轻头脑的熔炉,其极高的难度足以让各国的顶尖冠军都感到敬畏。
OpenAI 的模型不仅成功挤入了这一精英行列,其表现甚至还留有余地。
这一成果,标志着机器的符号操作能力与人类的创造性证明能力之间长期存在的鸿沟已被填平,它代表了人工智能推理能力发展的一个真正历史性拐点。
一键三连「点赞」「转发」「小心心」
欢迎在评论区留下你的想法!











