哈喽,大家好~
今儿咱们聊聊统计检验方法中,非常重要的卡方检验。
先说:什么是“统计检验”?
统计检验就是用数据来“检验”一个说法是不是成立。
打个比方:
你怀疑一枚硬币不是公平的(不一定是正反各一半),那你就收集若干次投掷结果,用统计检验看数据有没有足够证据反驳“硬币是公平的”这个说法。
流程很简单:
先提出无效假设(H₀)(通常是“没差别”或“没关系”)。 提出备择假设(H₁)(你想证明的)。 计算一个检验统计量(从数据算出的一个数)。 看这个数在对应的参考分布里处于什么位置(是不是很极端),或者看对应的 p 值。 根据显著性水平(比如 0.05)决定拒绝还是不拒绝 H₀,最后用自然语言说明结论。
卡方检验(Chi-square test)是什么?
卡方检验是用来处理类别数据的:例如“男/女”“吸烟/不吸烟”“A/B/C 三个品牌”等。它用来检验两类问题里的“差别”或“关系”是否显著。
常见两种情形:
拟合优度检验:检验观测到的类别频数,是否与某个理论(比如“均匀分布”或“厂家标称的比例”)一致。 独立性检验/列联表检验:检验两个分类变量(比如 性别 和 是否吸烟)是否相互独立(没有关联)。
它的核心公式很简单:
= 观测到的次数(Observed) = 在“没差别”的假设下预期的次数(Expected)
直观理解:每一格算一个 ,把这些“偏差程度”加起来,就是 χ² 值,值越大表示观测和预期越不一致。
自由度(degrees of freedom, df):
拟合优度:df = 类别数 k − 1(有时候还要减去估计参数个数) 独立性(r×c 表):df = (行数−1) × (列数−1)
最后把 χ² 值和相应自由度对应的卡方分布比较,或算 p 值,决定显著性。
先来两个例子,大家便于理解:
举例 1:掷 120 次骰子,想知道骰子是不是公平(拟合优度检验)
假设观察到的结果(每面点数出现次数)为:
1 点:8 次 2 点:20 次 3 点:22 次 4 点:18 次 5 点:26 次 6 点:26 次
总次数 = 120。理论上“公平骰子”每面期望次数 。
现在一步步代入公式计算(按每一面算贡献):
面 1:
面 2:
面 3:
面 4:
面 5:
面 6:同面 5,贡献 1.8
把这些加起来:
自由度 df = 6 − 1 = 5。
接下来比对卡方分布或者查表/软件(我们常用显著性水平 α = 0.05):
如果比临界值大,说明观测与“公平”差别显著 → 拒绝 H₀(骰子不公平)。 在这个例子中 = 11.2,稍微超过了 df=5 时 0.05 水平的临界值(大约 11.07),因此在 5% 显著性水平下我们会倾向于认为骰子可能不是公平的(但差别并不大,是“刚好”超过门槛)。
重要小提醒:这说明“有统计学证据不支持公平”,但要结合现实意义(是不是因为实验操作问题、样本量、还是偶然)来判断。
举例 2:性别(男/女)和是否吸烟(吸烟/不吸烟)有没有关系?(列联表、独立性检验)
观测到的数据(总样本 200 人):
先算每格的期望次数 :
男-吸烟: 男-不吸烟: 女-吸烟: 女-不吸烟:
逐格算贡献:
男-吸烟: 男-不吸烟:(即 ) 女-吸烟: 女-不吸烟:
加起来:
自由度 df = (2−1)×(2−1) = 1。
查表或比较临界值(df=1 时 α=0.05 的临界值约为 3.84),我们的 χ² = 2.67 小于 3.84,所以不能拒绝独立性假设:即没有足够证据表明性别与吸烟有统计学上的关联(换句话说,基于这份样本,性别和是否吸烟看起来是独立的)。
注意项
下面几个点,大家需要注意~
数据类型要对:卡方检验只针对分类(类别)数据,不能直接用来比较两个平均数(那时用 t 检验/ANOVA)。 样本独立:每个观测必须相互独立(比如不同人的回答),否则结果不可靠。 期望次数不能太小:通常每个格子的期望 最好 ≥ 5。如果很多格子小于 5,卡方近似不好,应该合并类别或改用 Fisher 精确检验(针对 2×2 表)。 2×2 表有校正:对于 2×2 表有时会用 Yates 校正,但现代做法通常直接用精确检验或统计软件给出的 p 值。 显著 ≠ 重要:样本很大时,很小的差别也可能显著;要看效应大小(例如 Cramér’s V),不要只盯 p 值。
完整案例实现
某公司对 200 名消费者做了问卷调查,想分析「购买产品类型」与「消费者地区」是否有关。
产品类型:A、B、C 地区:东部、中部、西部、北部
公司想知道,不同地区的人购买产品的比例分布是不是一致,还是有显著差异。
我们将使用 卡方独立性检验 来检验“产品类型与地区是否独立”。
分析步骤
构建一个 3×4 的列联表(虚拟数据)。 计算期望值 并手动算出卡方统计量。 基于自由度计算 p 值,并绘制卡方分布曲线,标记统计量位置。 数据分析可视化,直观展示数据差异与分布。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import chi2
# 1. 虚拟数据(3 产品类型 × 4 地区)
observed = np.array([
[25, 30, 20, 15], # 产品 A
[15, 25, 30, 10], # 产品 B
[10, 20, 25, 25] # 产品 C
])
products = ["A", "B", "C"]
regions = ["东部", "中部", "西部", "北部"]
df_obs = pd.DataFrame(observed, index=products, columns=regions)
# 2. 手动计算卡方统计量
total = observed.sum()
row_totals = observed.sum(axis=1).reshape(-1, 1)
col_totals = observed.sum(axis=0).reshape(1, -1)
expected = row_totals @ col_totals / total # 外积计算 E
chi2_stat = ((observed - expected) ** 2 / expected).sum()
dfree = (observed.shape[0] - 1) * (observed.shape[1] - 1)
p_value = 1 - chi2.cdf(chi2_stat, dfree)
print("观测值:\n", df_obs)
print("\n期望值:\n", pd.DataFrame(expected, index=products, columns=regions))
print(f"\nχ² 统计量: {chi2_stat:.4f}")
print(f"自由度: {dfree}")
print(f"p 值: {p_value:.4f}")
# 3. 绘制卡方分布曲线并标记统计量位置
x = np.linspace(0, chi2.ppf(0.999, dfree), 500)
plt.figure(figsize=(8,5))
plt.plot(x, chi2.pdf(x, dfree), color="orange", lw=2, label=f"卡方分布 (df={dfree})")
plt.axvline(chi2_stat, color="red", linestyle="--", lw=2, label=f"统计量 χ²={chi2_stat:.2f}")
plt.fill_between(x, chi2.pdf(x, dfree), where=(x >= chi2_stat), color="red", alpha=0.3)
plt.title("卡方分布与检验统计量位置", fontsize=14)
plt.xlabel("χ² 值")
plt.ylabel("概率密度")
plt.legend()
plt.show()
# 4. 数据分析可视化(4 张图)
# 图1:原始数据堆叠条形图
df_obs.plot(kind="bar", stacked=True, color=["#FF6347", "#FFD700", "#90EE90", "#1E90FF"], figsize=(8,5))
plt.title("不同产品在各地区的销量分布(堆叠)")
plt.ylabel("人数")
plt.show()
# 图2:期望 vs 观测 对比热力图
fig, ax = plt.subplots(1, 2, figsize=(12,5))
sns.heatmap(df_obs, annot=True, fmt="d", cmap="YlOrRd", ax=ax[0])
ax[0].set_title("观测值热力图")
sns.heatmap(pd.DataFrame(expected, index=products, columns=regions), annot=True, fmt=".1f", cmap="YlGnBu", ax=ax[1])
ax[1].set_title("期望值热力图")
plt.show()
# 图3:每列百分比堆叠条形图
df_pct = df_obs.div(df_obs.sum(axis=0), axis=1) * 100
df_pct.T.plot(kind="bar", stacked=True, figsize=(8,5), color=["#FF4500", "#32CD32", "#4682B4"])
plt.title("各地区不同产品的百分比分布")
plt.ylabel("百分比 (%)")
plt.show()
# 图4:残差热力图(标准化)
residuals = (observed - expected) / np.sqrt(expected)
sns.heatmap(pd.DataFrame(residuals, index=products, columns=regions), annot=True, cmap="coolwarm", center=0)
plt.title("标准化残差热力图(正值表示高于期望)")
plt.show()
# 图5:按地区总销量排序条形图
total_by_region = df_obs.sum(axis=0).sort_values(ascending=False)
total_by_region.plot(kind="bar", color="#FF69B4", figsize=(7,4))
plt.title("各地区总销量(人数)")
plt.ylabel("人数")
plt.show()
# 图6:按产品类型总销量排序条形图
total_by_product = df_obs.sum(axis=1).sort_values(ascending=False)
total_by_product.plot(kind="bar", color="#00CED1", figsize=(7,4))
plt.title("各产品类型总销量(人数)")
plt.ylabel("人数")
plt.show()
构造数据: observed是 3×4 的列联表,行是产品类型,列是地区。手算卡方统计量
用行总 × 列总 / 总数 得到期望值矩阵 expected。按公式 计算统计量。 自由度 (r-1)*(c-1),用scipy.stats.chi2计算 p 值。
chi2.pdf 绘制理论分布曲线,标出统计量位置,并在右尾区域填充颜色,显示拒绝域。
数据分析可视化
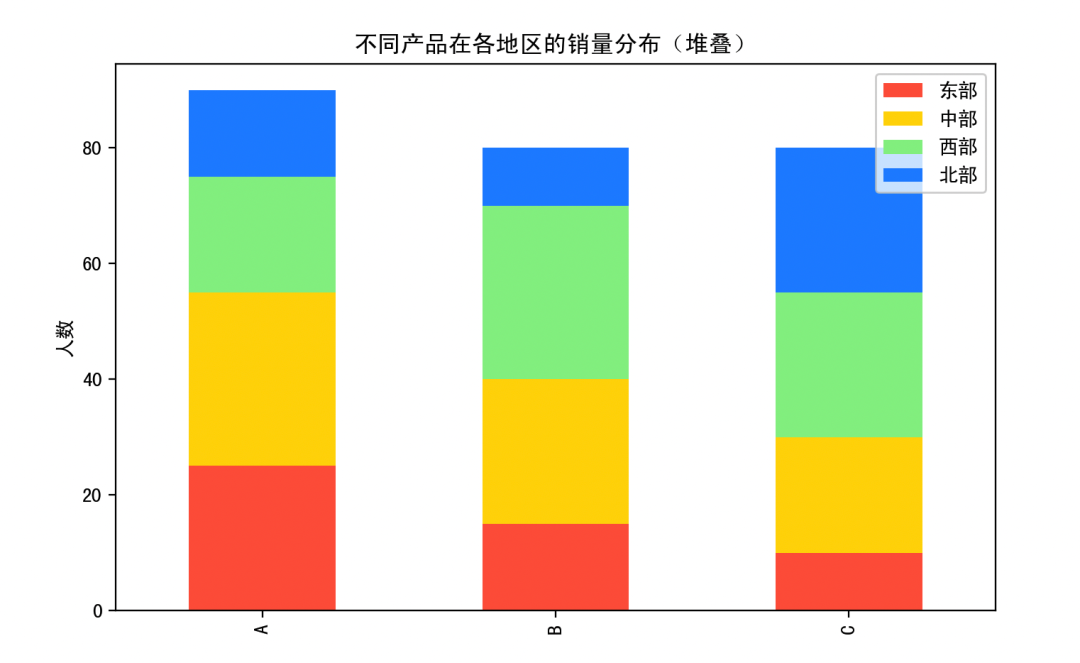
图1:原始销量堆叠条形图 → 看总体差异。

图2:观测值 & 期望值热力图 → 对比差异。

图3:百分比堆叠条形图 → 看结构比例差异。

图4:标准化残差热力图 → 高于或低于期望的位置。

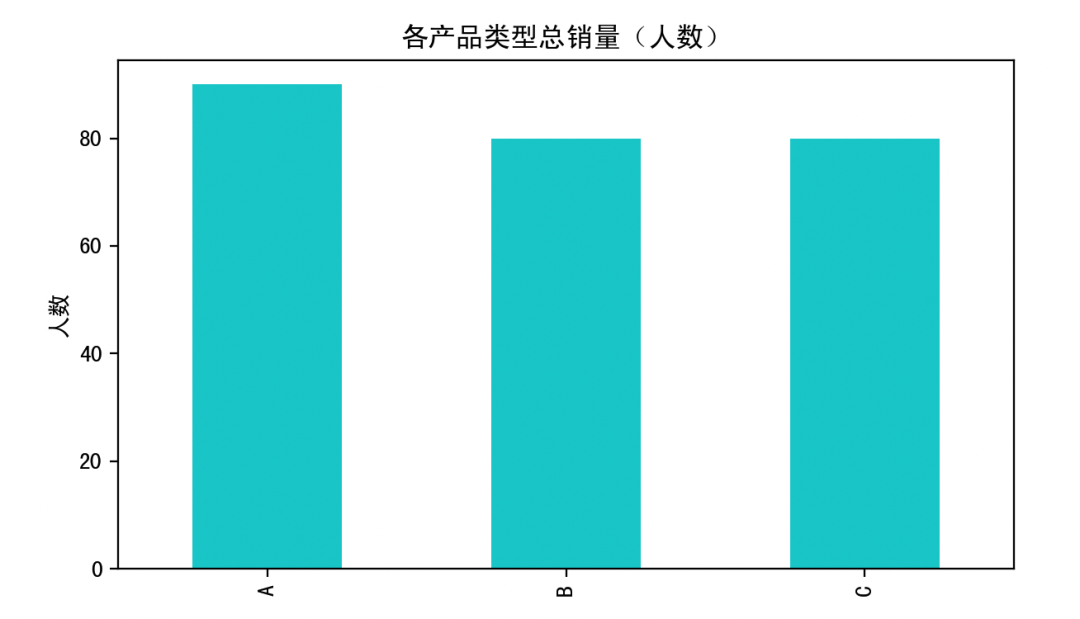
图5 & 图6:总销量排序条形图 → 发现销量最多的地区和产品类型。
我们做的这个小实验,看不同地区的人买产品类型是不是差不多,先用卡方公式算出统计量和 p 值,再画出卡方分布和一堆彩色图看看差异在哪。
结果一目了然:哪块儿买啥多、哪块儿买啥少~
最后
最近准备了16大块的内容,124个算法问题的总结,完整的机器学习小册,免费领取~












