混元3D团队投稿
量子位 | 公众号 QbitAI
全景图具有完整的视场 (360°×180°),比透视图提供更完整的视觉描述。得益于此特性,全景深度估计在3D视觉领域正日益受到关注。
然而,由于全景数据的稀缺,以往的方法通常局限于域内设置,导致零样本泛化能力较差。此外,由于全景图固有的球面畸变,许多方法依赖于透视分割(例如,cubemaps,立方体贴图),这导致效率不理想。
为了应对这些挑战,腾讯混元3D团队提出了DA2,一个准确的、零样本泛化能力强且完全端到端的全景深度估计器。

背景与挑战
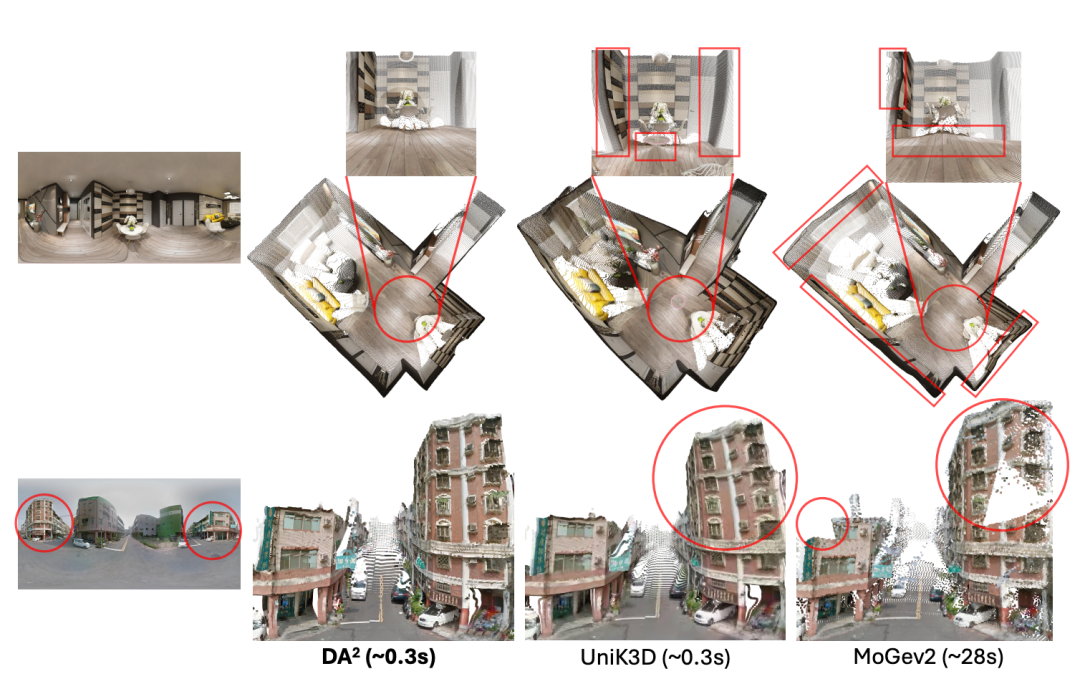
△图1:Teaser图片
与常用的透视图像不同,全景图提供沉浸式的360°×180°视角,可从“任何方向”(Any Direction)捕捉视觉内容。
这种宽阔的视场使全景图成为计算机视觉领域中必不可少的视觉表示,并赋能了各种激动人心的应用,例如AR/VR和沉浸式图像生成。
然而,仅有沉浸式视觉(二维)体验是不够的。全景图中的高质量深度 (3D) 信息对3D场景重建/生成、物理模拟、世界模型等更高级的应用至关重要。
受此启发,腾讯混元3D团队专注于以端到端的方式估计从每个全景像素到球体中心(即360°相机)的scale-invariant[1]和distance[2],并实现高保真度和强大的零样本泛化。
[1] Distance(距离)和depth(深度)具有三种类别,分别是metric,scale-invariant (biased), 和affine-invariant (relative)。Metric是指具有绝对scale(尺度)的绝对深度,是最严格的定义。scale-invariant是指不具备绝对尺度的深度,但是具有全局的shift(or bias,偏差),也是很严格的定义,metric和scale-invariant都可以完整保存具体的3D结构。affine-invariant是最松的定义,它不能保存完好的3D结构,主要表达的是不同像素的前后深度顺序。
[2] 严格来讲,distance(距离)为: ,depth(深度)为z。这里使用depth是为了更好的可读性和连贯性。
,depth(深度)为z。这里使用depth是为了更好的可读性和连贯性。
挑战在于:
拍摄或渲染全景图比透视图更具挑战性,因为全景深度数据的数量和多样性都非常有限。因此,早期的方法大多是在领域内进行训练和测试,零样本泛化能力非常有限。 由于全景图固有的球面畸变,许多方法融合了ERP(1个全景图)和立方体贴图(6个透视视角)投影的特征。这些策略虽然有效,但仍然需要额外的模块,因此不够精简,效率也不够高。
核心贡献
这项工作的首要目标是扩展全景数据,并为DA2构建坚实的数据基础。
腾讯混元3D团队首先想到的,是基于大量高质量的透视深度数据,转换得到全景数据。为此,他们提出了一个数据管理引擎,将透视样本转换为高质量的全景数据。

△全景数据扩充引擎
具体来说,给定一个已知水平和垂直视场角的透视RGB图像,首先应用透视到等距矩形(Perspective-to-Equirectangular,P2E)投影将图像映射到球面空间。
然而,由于透视图像的视场角有限(水平范围通常为70°-90°),因此只能覆盖球面空间的一小部分(如图2左侧球体所示)。因此,这样的P2E投影图像可以被视为“不完整”的全景图。这种不完整性会导致性能不佳:1)该模型缺乏全局背景,因为它从未观察到全景图像的全貌,尤其是在两极附近;2)球面畸变在赤道和两极之间差异很大,高纬度地区会出现严重的拉伸。
为此,研究团队将使用全景图的外推引擎进行全景外推,以生成与模型输入匹配的“完整”全景图。对于相关的GT深度,研究团队仅应用P2E投影,而未进行外推,因为外推深度的绝对精度很难得的保证。总体而言,该数据扩充引擎显著提升了全景数据的数量和多样性,并显著增强了DA2的零样本性能,如图3所示。
△图3:模型性能与数据规模的曲线
该数据扩充引擎创建了约543K个全景样本,将样本总数从约63K扩展到约607K(约10倍),显著解决了数据稀缺导致泛化能力差的问题。
接下来,研究团队重点关注DA2的模型结构和训练,以便有效地从大幅扩展的数据中进行学习。
△图4:SphereViT 架构及其训练损失
为了减轻球面畸变的影响,受Vision Transformers (ViT) 中位置嵌入的启发,研究团队提出了SphereViT——DA2的主要模型架构。
具体来说,从球体布局出发,研究团队首先计算以相机为中心的球面坐标系中每个像素的球面角(方位角和极角)。
然后,使用正弦-余弦基函数将这个双通道角度场扩展至图像特征维度,从而形成球面嵌入(Spherical Embedding)。由于所有全景图都具有相同的完整视场,因此该球面嵌入可以固定且可重复使用。为了注入球面感知,只需让图像特征去“关注”球面嵌入,而不必反过来。也就是说,SphereViT并非像标准ViT那样在自注意力机制之前将位置嵌入添加到图像特征上,而是采用交叉注意力机制:将图像特征视为查询,将球面嵌入视为键和值。这种设计使图像特征能够明确地关注全景图的球面几何形状,从而产生可感知畸变的表示并提升性能,如图5(a)所示。
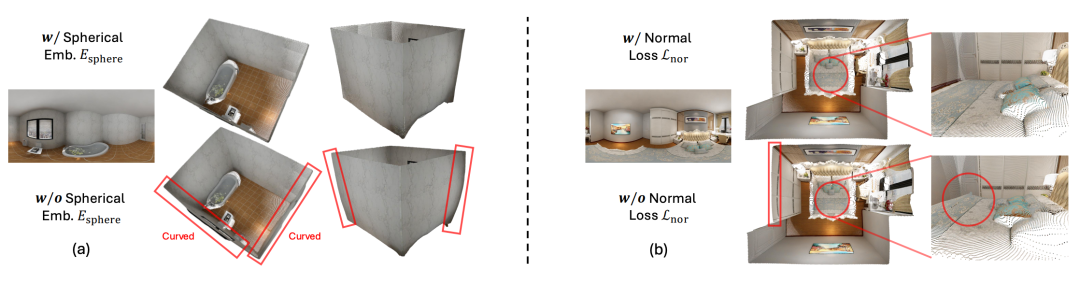
△图5:消融研究
在训练过程中,模型的监督机制结合了两个方面:距离损失约束全局精确的距离值;法线损失促进局部平滑、锐利的几何表面,尤其是在距离值相似但表面法线差异较大的区域,如图5(b)所示。
实验结果
为了验证DA2,研究团队结合多个公认的评估数据集,对尺度不变距离进行了全面的基准测试。
△表1:定量比较
然而,由于全景数据的稀缺,现有的全景深度估计零样本方法有限,而在透视深度估计方面,存在许多强大的零样本方法。因此,为了确保更公平、更全面的比较,研究团队遵循MoGe (https://github.com/microsoft/moge)提出的全景深度估计流程,并将DA2与先前的零样本透视深度估计器(Metric3D v1v2、VGGT、UniDepth v1v2、ZoeDepth、DepthAnuthing v1v2、Lotus、MoGe v1v2)也引入了基准测试。
如表1所示,DA2展现出了SOTA性能,其AbsRel性能比最强的zero-shot方法平均提升了38%。
值得注意的是,它甚至超越了之前的in-domain方法,进一步凸显了其卓越的泛化能力。
△图6:定性比较
研究团队还进行了定性比较,如图6所示。得益于本文提出的数据管理引擎,DA2训练所用的全景数据比UniK3D多出约21倍,展现出更精确的几何预测。DA2也优于MoGev2,因为后者的全景性能受到融合过程中多视角不一致性(例如不规则墙壁、破碎的建筑物等)的限制。
应用场景
DA2凭借其卓越的零样本泛化全景深度估计能力,有效地实现了广泛的3D重建相关应用,例如全景多视图重建。
如图7所示,DA2能够根据房屋/公寓不同房间的全景图像,重建全局对齐的3D点云,确保不同房间的多个全景视图之间的空间一致性。