点击下方卡片,关注「3D视觉工坊」公众号
选择星标,干货第一时间送达
本文经作者授权发布 | 来源:3D视觉工坊
星球内新增20多门3D视觉系统课程、入门环境配置教程、多场顶会直播、顶会论文最新解读、3D视觉算法源码、求职招聘等。想要入门3D视觉、做项目、搞科研,欢迎加入!
3D Gaussian Splatting(3DGS)自从提出以来,凭借高效率和高质量的特点,已经在显式三维重建领域产生了很大影响。不过,它仍然存在一个长期被忽视的问题:3DGS 的参数化表达并不“适合神经网络”。
如果你尝试过直接用高斯参数去训练神经网络(如前馈网络),大概率会遇到训练不稳定、难以收敛等情况。这并不是实现细节的问题,而是表示方式本身带来的困难。
在ICLR 2026的论文Learning Unified Representation of 3D Gaussian Splatting中,作者提出了一种新的Submanifold Field(SF)表示。这种表示为3DGS提供了一个稳定、唯一、规整的表示空间,使其更容易与神经网络结合和学习。
作者团队:
Yuelin Xin, Yuheng Liu, Xiaohui Xie, Xinke Li
作者单位:UC Irvine, City University of Hong Kong
项目主页:https://cilix-ai.github.io/gs-embedding-page/
项目代码:https://github.com/cilix-ai/gs-embedding
arXiv:https://arxiv.org/abs/2509.22917
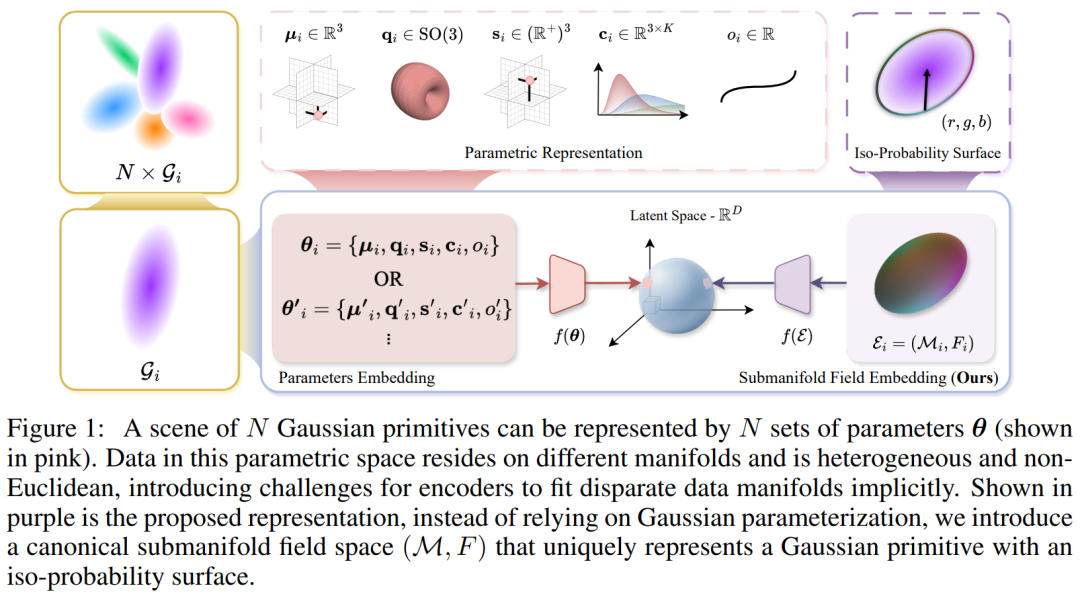
挑战:参数化学习为何会失效
直接使用原始的高斯参数进行学习,本身就存在结构性问题。首先,这些参数是异构的,而且并不唯一。一个最典型的例子就是“多对一”的映射问题。比如在旋转表示中,四元数q和-q虽然数值不同,但对应的是完全相同的几何状态。 从数学角度看,不同类型的高斯参数分布在不同的流形上,例如旋转位于 SO(3),尺度位于。这种不一致的参数空间,会在学习过程中带来表示冲突:神经网络的编码器 E(⋅)很难把“数值不同、但物理意义相同”的参数映射到同一个潜在表示点上。形式化地说,即使两个参数集合描述的是同一个物理高斯,也可能出现:
这正是直接对3DGS参数做学习时,训练不稳定、难以收敛的重要原因之一。
我们的解决方案:Submanifold Field Embedding
与其依赖不稳定的参数化方式,我们提出了Submanifold Field(M,F)。核心思路是:不再直接用参数来定义一个高斯,而是用它的等概率曲面来刻画——这是一种在三维空间中具有规范形式的子流形。具体来说,一个三维高斯由如下密度函数定义:
我们选择一个固定的概率阈值τ,将满足 g(x)=τ的点集视为子流形M,并在其上定义对应的颜色场F。这种几何化的表示方式,保证了高斯的物理形状与其表示之间存在严格的一一对应关系,从根本上避免了参数层面的多对一问题。
为了让这一表示真正可用于神经网络学习,我们进一步设计了SF-VAE(Submanifold Field Variational Auto-encoder)。它可以将任意输入的子流形场离散化为一个点云,并映射为一个紧凑的32维向量(或更低维向量)表示:
随后,解码器再从这个平滑的欧式潜空间中重建出对应的高斯参数 θ,从而实现稳定、连续、对学习友好的表示与生成过程。

主要发现与实验结果
1.显著提升的重建质量
在新的表示空间中进行学习后,SF-VAE 在重建质量上取得了非常明显的提升。以 ShapeSplat 数据集为例,使用前馈网络学习原始高斯参数时,重建结果的 PSNR 只有 37.5;而在采用 SF 表达之后,这一数值提升到了63.4。
这个结果说明,统一且对神经网络友好的表示方式,可以极大释放 3D Gaussian 在基于学习的前馈网络重建质量上的潜力,而提升并不是来自更复杂的模型,而是来自更合理的表示本身。


2.零样本泛化能力
一个相当出人意料的结果是,我们的方法几乎不依赖具体数据域。即使 只在随机生成的合成高斯数据集上训练,SF-VAE也依然能够在复杂的真实场景中表现良好(zero-shot)。
例如,在完全没有见过真实场景数据的情况下,模型依然可以直接泛化到 Mip-NeRF 360这样的真实世界数据集上,且重建效果几乎不受影响。这说明,Submanifold Field Embedding 捕捉到的是高斯本身的几何结构,而不是某一类数据分布的统计特征。

3.对噪声的鲁棒性
在许多下游任务中,模型预测得到的embedding往往不可避免地会包含噪声。为此,我们在设计 SF embedding 时,刻意强调了表示的平滑性和连续性。
实验中的行为分析表明,即使在噪声水平较高的情况下,SF-VAE 依然能够很好地保持高斯的几何结构;相比之下,直接基于参数的模型在这种条件下往往会更容易失效。我们通过如下Manifold Distance来评估高斯之间的偏差:
结果显示,SF embedding对噪声的敏感性显著更低,这也是其在复杂下游任务中表现更稳定的重要原因。


超越重建:面向下游任务的应用
SF Embedding不只是用于提升重建质量,它还能捕捉3D高斯中更深层的语义结构,这也为一系列下游应用打开了新的空间。
首先,在无监督语义聚类任务中,基于 Submanifold Field 的嵌入相比原始高斯参数,能够更好地保留局部和整体的语义信息,使得相似语义结构在嵌入空间中自然聚集。
其次,在Gaussian Neural Fields(GNF)场景下,SF Embedding 可以作为一个数值上更稳定的学习目标,用于基于前馈神经网络的重建任务。这一点在实际训练中尤为重要,因为它显著降低了由参数不连续性带来的优化困难。


本文仅做学术分享,如有侵权,请联系删文。
3D视觉硬件

3D视觉学习圈子
星球内新增20多门3D视觉系统课程、入门环境配置教程、多场顶会直播、顶会论文最新解读、3D视觉算法源码、求职招聘等。想要入门3D视觉、做项目、搞科研,欢迎扫码加入!

3D视觉全栈学习课程:www.3dcver.com

3D视觉交流群成立啦