神经网络求解 PDE 有多猛？顶会顶刊+工业落地双丰收！现在还在疯狂出成果

神经网络求解PDE是近年来科学计算领域的革命性突破，它融合了深度学习与物理建模的优势，解决了传统数值方法需要复杂网络划分和大量计算的缺陷，实现了速度与效率的双重提升！

因此，这方向不仅众多场景都适用，在各顶会顶刊的接受度也相当高，堪称学术圈 “流量密码”！尤其适合想发论文、搞落地的同学。目前，这方向论文潜力主要集中在物理嵌入可解释性、多尺度动态建模、低成本训练等，如果有论文er感兴趣，建议从这些角度入手。

当然，写论文必少不了参考，为方便大家学习，我特别整理了12篇神经网络求解PDE最新论文，开源代码已附，希望可以给到大家一点帮助。

扫码添加小享，回复“神经PDE”  

免费获取全部论文+开源代码

VW-PINNs: A volume weighting method for PDE residuals in physics-informed neural networks

方法：论文提出了一种新的神经网络方法（VW-PINNs），通过在PINNs中引入体积加权残差来改进PDE求解。它解决了非均匀采样点下PINNs收敛效率低的问题，通过加权PDE残差确保了整个计算域内的充分收敛，提升了求解偏微分方程的效率和准确性。

创新点：

• 提出体积加权残差（VW-PINNs），通过采样点体积加权PDE残差，解决非均匀采样下PINNs收敛问题。
• 开发核密度估计体积近似算法，适用于无网格随机采样，高效计算采样点体积。
• 经流体力学和Burgers方程实验验证，VW-PINNs在求解效率、收敛性和准确性上显著提升。

Quantum physics informed neural networks for multi-variable partial differential equations

方法：论文提出了一种量子物理信息神经网络（QPINNs），利用量子计算和机器学习相结合的方法来求解PDEs。它通过设计一种新的量子神经网络架构，直接计算高阶导数，避免了嵌套微分带来的复杂性，显著提升了求解效率和精度。

创新点：

• 提出量子物理信息神经网络（QPINNs），结合量子计算和机器学习，用于求解PDEs。
• 设计了一种新的量子神经网络架构，能够直接计算高阶导数，避免了嵌套微分带来的复杂性。
• 通过求解一维热方程验证了QPINNs的有效性，展示了其在处理PDEs方面的潜力。

Synergistic Learning with Multi-Task DeepONet for Efficient PDE Problem Solving

方法：论文提出多任务深度算子网络（MT-DeepONet），扩展传统框架，实现单次训练学习多任务（如不同参数、几何形状的PDE解）。通过二值掩码和改进结构，提升模型泛化与知识迁移能力。

创新点：

• 提出多任务深度算子网络（MT-DeepONet），能够在单次训练中同时学习多个偏微分方程的不同参数条件和几何形状。
• 引入二值掩码技术，改善了模型在不同几何形状下的收敛性和泛化能力。
• 通过多个基准问题验证了该方法在处理多任务PDE问题时的高效性和准确性。

Physics-informed neural networks with hybrid Kolmogorov Arnold network and augmented Lagrangian function for solving partial differential equations

方法：论文提出了一种新型的神经网络模型AL-PKAN，用于求解PDEs。该模型结合了KAN和增广拉格朗日函数，通过将输入序列编码到高维潜在空间并进行精细解码，显著提高了求解PDEs的精度和稳定性。

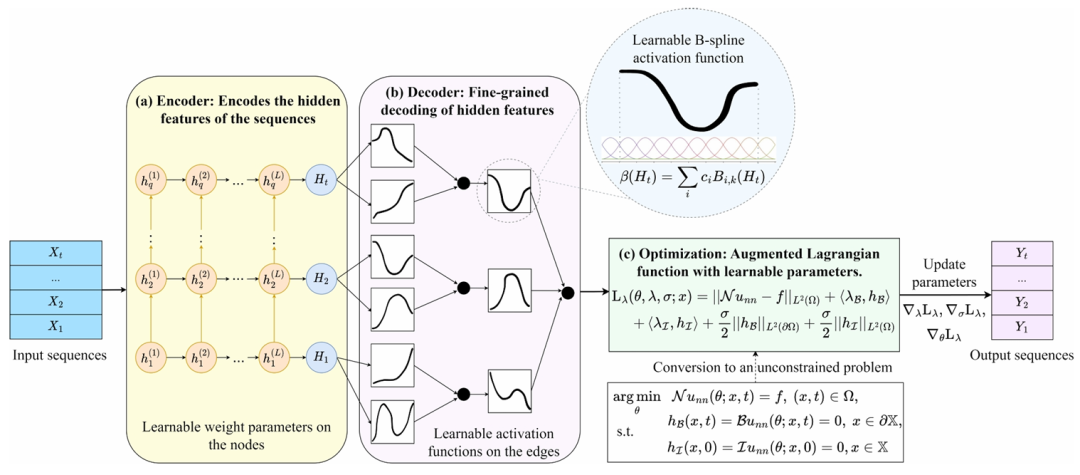
创新点：

• 提出了一种新型混合模型AL-PKAN，结合了KAN和增广拉格朗日函数，用于高效求解PDEs。
• 通过将输入序列编码到高维潜在空间并利用KAN进行解码，显著提高了模型的可解释性和非线性拟合能力。
• 重构了损失函数，避免了传统方法中惩罚因子无限增长的问题，显著提高了模型的优化稳定性和收敛性。