
DV−Hop 定位算法基于距离矢量路由原理,是非测距的定位算法,也称为距离向量跳段定位算法。DV−Hop 定位算法的优化策略主要针对算法本身的 3 个步骤进行改进,即最小跳数的选取、平均跳距的计算和未知节点坐标的计算。
国内外学者在此基础上提出了大量的改进方案。Kumari 等通过将工作区域分为等大小球形带以修正最小跳数,提高了定位精确度。刘川洲等采用了多种方法对经典 DV−Hop 算法的 3 个步骤分别进行了优化,提高了定位精度。随着人工智能算法的不断涌现,出现了将智能算法引入到 DV−Hop 算法中的改进方案。刘燕等在 DV−Hop 算法中引入了人工蜂群算法,并在多边定位阶段引入数学优化模型,以解决 DV−Hop 算法定位误差较大的问题。孙博文等将改进的灰狼优化算法与 DV−Hop 算法融合,在一定程度上解决了基于群智能的 DV−Hop 算法性能不理想的问题。Liu 等设计了一种基于多目标樽海鞘群优化的 DV−Hop 算法,利用改进的多目标樽海鞘算法估计节点坐标。
目前基于 DV−Hop 算法的改进,虽然在某种程度上能够取得较好的定位效果,但很多算法的改进都是在原算法的基础上引入其他更加复杂的算法。无线传感器网络节点硬件资源通常有限,若将最小二乘法替换为智能优化算法,在实际应用中对节点的计算开销提出了更高的要求。因此,基于轻量化、低复杂度的优化思路,从多通信半径最小跳数优化与跳距加权修正 2 个方面对传统 DV−Hop 定位算法进行改进,并通过仿真实验验证其有效性。
传统 DV−Hop 算法是非测距的定位算法,它利用包含最小跳数等位置信息的广播数据包,来计算节点间的距离估计值,并进一步求解未知节点的坐标。在 DV−Hop 算法中,锚节点首先在网络中广播自身的位置信息。当其他节点接收到这些信息时,会以此来更新自身最小跳数、跳距等信息,并将新数据再次广播。通过这种机制,所有未知节点都可以获得锚节点包含最小跳数的数据包。DV−Hop 算法的具体步骤如下。
步骤 1:网络初始化,跳数初始化为 0。
步骤 2:锚节点计算平均跳距。计算如式 (1)

式中,锚节点 i 与锚节点 j 的坐标值分别为(xi, yi)和(xj,yj),两者之间的最小跳数为 Hopij (i ≠ j)。
步骤 3:锚节点向通信半径 R 内的未知节点广播自身的数据。
步骤 4:若未知节点接收到数据,判断其是否为记录过的数据包,若未记录过,保存该数据包,将到该锚节点的最小跳数设为 1;若记录过,则将该跳数加 1 后转发给邻居节点。
步骤 5:若邻居节点接收到的转发数据包来自相同锚节点,则只保存到该锚节点最小的跳数值与对应的平均跳距。
步骤 6:未知节点计算与锚节点的距离,如式 (2)和式 (3) 所示

式 (2)、式 (3) 中,Hopsizej 为未知节点 j 的平均跳距,Hopsizei 为未知节点 j 第一次接收到的锚节点 i 的平均跳距,未知节点 j 和锚节点 i 之间的计算距离为 dij,未知节点 j 和锚节点 i 之间的最小跳数为Hopij。
步骤 7:当未知节点接收到 3 个或以上的锚节点数据时,计算位置坐标。由式 (3) 得到锚节点与未知节点之间的估计距离 dk 后,根据式(4) 求解估计坐标

式中,未知节点的坐标为(x, y),锚节点的坐标为(xk, yk),k=1,2,…N。式 (4) 可通过式 (5) 表示

式中,

如式 (9),坐标X通过最小二乘法求解

式中,T 为矩阵的转置。
2.1 多通信半径最小跳数的优化
在传统 DV−Hop 算法中,会出现节点实际距离相差很大,但最小跳数值却相同的情况。若 2 个节点之间的距离小于或等于锚节点的通信半径,2 个节点与锚节点之间的最小跳数值均为 1。而在实际网络中,这 2 个节点到该锚节点的实际距离却可能相差很大。这即是最小跳数值引起的误差。
对于锚节点通信半径内的多个未知节点之间因最小跳数选取而引起的误差,采取通信半径分层的方法进行优化。提出的锚节点通信半径分层示意图如图 1 所示。
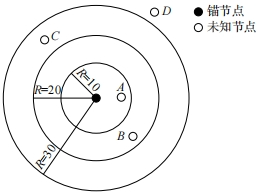
图 1 节点通信半径分层示意图
设锚节点的通信半径为 R,将其分为 m 个层级,锚节点可按划分的层级数依次广播。此时位于不同广播半径内的未知节点与锚节点之间的距离为 d。i 为正整数,满足 i∈[1, m]

根据式 (10),若取 R=30,m=3,则图 1 中的节点A、B、C、D 与锚节点之间的最小跳数值分别为 1/3、2/3、1、4/3。显然,通过改进,锚节点和未知节点之间的最小跳数不再是整数值,而是与距离更接近正比例关系的小数值,从而达到减小定位误差的目的。
2.2 跳距的加权修正
在传统 DV−Hop 算法中,未知节点使用与其最近的锚节点平均跳距作为自身的平均跳距,并通过最小跳数和平均跳距相乘计算与其他节点的距离。然而节点不规则分布导致的网络拓扑不规则,产生了大量由折线路径组合的通信路径。通过平均跳距计算的距离与实际距离不符,使误差累积,降低了定位精度。本文采用跳距加权的方法对误差进行修正。
设未知节点坐标为 D(x,y),与该未知节点通信的锚 节 点 的 坐 标 分 别设为 A1(x1,y1), A2(x2,y2), … ,An(xn,yn)。这些锚节点的平均跳距分别为 hopsize1,hopsize2,…,hopsizen。各个锚节点到未知节点 D(x,y)的跳数分别为 hop1,hop2,…,hopn。未知节点 D(x,y)到锚节点 A1(xi, yi)的距离 ri 如式 (11) 所示

对于未知节点与其他节点间的距离估算,基于其最小跳数与其平均跳距的乘积。通过对未知节点平均跳距加权处理,可以减少误差。平均跳距修正公式如式 (12)~(14) 所示

由式 (12) 可知,若锚节点距离未知节点越近,其hopi越小,得到的权值ωi就会越小,由式 (13) 得出修正后的hopsizei值与原来的值相差就会越小,从而在式(14) 中求平均跳距时的占比会越大。通过对每个与未知节点通信的锚节点平均跳距进行加权,能有效提高定位精度。
综合以上 2 个方面的改进,本文提出的基于多通信半径最小跳数优化与跳距加权修正的 DV−Hop 定位算法流程图如图 2 所示。

图 2 基于多通信半径最小跳数优化与跳距加权修正的 DV−Hop 定位算法流程
3.1 仿真环境及参数
采用 Matlab2016B 对改进 DV−Hop 算法进行验证。环境为100 m×100 m 的二维区域,仿真次数为100,求取平均值作为最终结果以减少随机性带来的影响。仿真环境中的参数设置如表 1 所示。
评估算法性能的标准是归一化定位误差,如式(15) 所示

式中,R 为网络通信半径,N 为未知节点总数,(xir,yir)和(xie,yie)分别代表第 i 个未知节点的实际位置坐标和预测位置坐标。
表 1 仿真环境参数设置

3.2 算法性能仿真与结果分析
为了验证算法的性能,采用改进的 DV−Hop 算法与传统 DV−Hop 算法、文献的算法进行对比分析。节点总数、锚节点占比和节点通信半径对 2 种算法的定位精度有着很大的影响。其中增加节点数量可以提高网络拓扑中未知节点接收到数据的概率,从而提高定位精度,提高锚节点占比可以让未知节点接收到更多锚节点数据,从而提高定位精度,而增加节点通信半径可以减少网络拓扑中折线段的数量,从而提高定位精度。在后续的仿真中将通过这 3 个变量对实验结果进行分析。
1) 节点总数对定位精度的影响。选定节点总数作为变量,从初始值 50 开始以步长 5 升至 100,改进DV−Hop 算法的通信半径分级层数分别设置为 m=2、m=3、m=4、m=5,锚节点占比统一确定设置为 30%,通信半径设为 50 m,仿真结果如图 3 所示。

图 3 不同节点总数的定位误差
由图 3 可知,定位误差与节点总数在整体上成反比,且不断趋于稳定。这是因为在固定的有限区域内,节点的总数越多,单位面积内的节点密度越大,节点间的多跳折线段就越逼近直线。同时,通信半径的分层级数也与定位误差成反比。当 m=2 和 m=3 时,定位误差明显减小,当 m=4 和 m=5 时,定位误差减小较少。m=2 时改进算法较传统 DV−Hop 算法的平均定位误差减小了约 27%;m=2 较 m=3 时算法平均定位误差减小了约 12%;m=4 较 m=3 时算法定位误差减小幅度小于其他情况,这是因为通信半径分层级数越 多, 跳 数 选 择 产 生 的 误 差 会 越 来 越 小 。 其 中m=5 时总体的归一化误差较文献的算法减小了22%。
2) 锚节点占比对定位精度的影响。选定锚节点占比为变量,从初始值 5% 开始以步长 5% 升至 50%,改进 DV−Hop 算法的通信半径分级层数分别设置为m=2、m=3、m=4、m=5,节点总数统一设置为 100 个,通信半径设为 50 m,仿真结果如图 4 所示。

图 4 不同锚节点占比的定位误差
由图 4 可知,随着锚节点占比的增加,改进算法与传统 DV−Hop 算法的平均定位误差均会逐渐降低。在固定有限区域内,锚节点数量越多,未知节点接收到的锚节点数据就会越多,位置求解越精确。通信半径的分层级数也极大降低了定位误差。在锚节点占比为 5%~15% 时,定位误差受锚节点占比影响较大,当锚节点占比超过 15% 后,定位误差变化均趋于稳定。同样,通信半径分级层数 m=2 和 m=3 时,定位误差减小效果较明显;当 m=2 时改进算法平均定位误差较传统 DV−Hop 算法减小了约 33%; m=3 较 m=2 时 改 进 算 法 平 均 定 位 误 差 减 小 了 约 11%;m=4 与 m=5 时平均定位误差的减小幅度较小,这是因为通信半径分层级数越多,跳数选择产生的误差会越来越小。其中 m=5 时总体的归一化误差较文献的算法减小了 14.37%。
3) 通信半径对定位精度的影响。选定通信半径作为变量,从初始值 20 m 开始以步长 5 m 升至 50 m,改进 DV−Hop 算法的通信半径分级层数分别设置为m=2、m=3、m=4、m=5,节点总数统一确定设置为100 个,锚节点占比设为 30%,仿真结果如图 5 所示。

图 5 不同通信半径的定位误差
由图 5 可知,随着通信半径的增加,2 种算法的平均定位误差都显著降低。当通信半径接近 30 m 时,定位误差趋于平缓;当通信半径接近 40 m 时,不同层级数的平均定位误差都趋于 10%。同样,m=2 时改进算法较传统 DV−Hop 算法平均定位误差减小了约27%;通信半径分级层数 m=2 和 m=3 时,平均定位误差显著减小,约为 19.4%。m=3 较 m=2 时平均定位误差减小了约 10.5%;m=4 和 m=5 时定位误差相差
无几,这是因为通信半径分层级数越多,跳数选择产生的误差会越来越小。其中 m=5 时总体的归一化误差较文献的算法减小了 27.25%。
4) 节点定位误差。根据上述实验分析可知,节点总数、锚节点占比和通信半径对改进 DV−Hop 算法和传统 DV−Hop 算法的定位精度都有着很大的影响。为对比改进前后定位算法的不同效果,在相同环境下,通过 2 种算法对未知节点进行定位。设置二维平面 100 m×100 m,节点总数 100 个,锚节点占比为20%,通信半径 30 m,求取平均位置误差进行对比,定位结果如图 6 所示。
由图 6 可知,80 个未知节点的平均定位误差在一定范围内呈现不规则的变化。其中,改进 DV−Hop 算法、传统 DV−Hop 算法、文献算法的定位误差均值分别为 3.8971、9.1843、4.6654 m。因此,所提出的算法具有最高的定位精度。

图 6 节点定位误差对比
针对传统 DV−Hop 定位算法存在较大定位误差的问题,提出了基于多通信半径最小跳数优化与跳距加权修正的 DV−Hop 定位算法。
1) 为改善 DV−Hop 算法中最小跳数选取造成的误差,提出了锚节点通信半径分层的方法来修正节点间的最小跳数。仿真结果表明,当分层级数 m=2 时,对比 DV−Hop 算法,改进 DV−Hop 算法的平均定位误差有显著降低。然而随着分层级数的增加,因跳数选择产生的误差越来越小,改善效果会逐渐减小。
2) 在 DV−Hop 算法中,未知节点采用与其最近锚节点的平均跳距作为自身跳距进行距离计算,为改善该步骤产生的误差,提出了加权平均跳距的方法修正未知节点的平均跳距。仿真结果表明,结合了多通信半径最小跳数优化与跳距加权修正的 DV−Hop 算法有效降低了节点的平均定位误差。
3) 在改进 DV−Hop 算法中,要求锚节点按层级数多次发送数据包,这增加了硬件的能量开销,而仿真结果表明,随着层级数的增加,定位误差的减小幅度会逐渐降低。同时,为了实现平均跳距的加权,要求未知节点进行多次较复杂的计算。因此,如何进一步平衡无线传感器网络的能耗与定位精度将是未来研究的重点。
本文作者:张烈平,黄自晨,尹亚梦,谭铭扬,王守峰
作者简介:张烈平,桂林航天工业学院机电工程学院,教授,研究方向为传感器与智能信息处理技术。


内容为【科技导报】公众号原创,欢迎转载
白名单回复后台「转载」
精彩内容回顾
《科技导报》创刊于1980年,中国科协学术会刊,主要刊登科学前沿和技术热点领域突破性的研究成果、权威性的科学评论、引领性的高端综述,发表促进经济社会发展、完善科技管理、优化科研环境、培育科学文化、促进科技创新和科技成果转化的决策咨询建议。常设栏目有院士卷首语、科技新闻、科技评论、专稿专题、综述、论文、政策建议、科技人文等。











